Из данных, входящих в выборку 
(табл.14.1.1) находим 
и 
, соответственно наименьшее и наибольшее значения выборки, и вычисляем число 
, называемое размахом выборки.
Размах выборки – это длина основного интервала, в который попадают все значения выборки. Далее значения 
, называемые вариантами можно упорядочить, то есть расположить в порядке возрастания. Тогда выборка 
, записанная по возрастанию, называется вариационным рядом. По формуле
, (14.2.1)
где 
целая часть числа 
, определим число 
.
Данное число задает количество подынтервалов, на которые разбиваем основной интервал 
. Вычисляем длину подынтервалов по формуле
(14.2.2)
и затем – границы подынтервалов:
. (14.2.3)
Находим 
частоты 
относительные частоты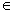
попадания значений выборки в 
й подынтервал. Причем должно быть 
.
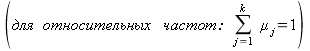В результате проведенных расчетов, получаем две таблицы:
Таблица 14.2.1
| |
 |
 |
… |  |
 |
 |
 |
… |  |
Таблица 14.2.2
| |
|
|
… | |
 |
 |
 |
… |  |
Далее, если найти середины подынтервалов:
, то получим еще одну таблицу.
Таблица 14.2.3
| |
 |
 |
… |  |
| |
 |
 |
… | |
В целях наглядности полученных в табл. 14.2.1, 14.2.2, 14.2.3 данных пользуются различными способами их графического изображения. К ним относятся гистограмма и полигон.
Для построения гистограммы относительных частот используем данные табл. 14.2.2. В декартовой системе координат на оси 
находим значения и и тем самым находим границы основного интервала, в который попадают все значения выборки. Затем на этом интервале откладываем границы подынтервалов. По оси 
откладываем величины 
(плотности вероятностей) 
. Тогда гистограммой относительных частот назовем ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные подынтервалы длины 
, а высоты равны числам 
(плотности вероятностей) . Аналогично, по данным табл. 14.2.1, строится гистограмма частот.
Для построения полигона относительных частот используем данные табл. 14.2.3. В декартовой системе координат на оси находим и , то есть изображаем границы основного интервала. Затем наносим значения середин подынтервалов 
. По оси откладываем значения, соответствующие относительным частотам 
.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 
.
Данные табл. 14.2.3 представляют эмпирический закон распределения выборки, а полигон относительных частот есть его визуальное представление.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию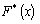 
, определяющую для каждого значения 
относительную частоту события 
.
Таким образом, 
, где 
число вариант, меньших , 
объем выборки.
Для каждой реализации выборки эмпирическая функция распределения однозначно определена и обладает всеми свойствами теоретической функции распределения:
1) значения эмпирической функции принадлежат отрезку 
;
2) 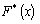не убывающая функция;
3) если 
наименьшая варианта, то 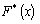= 0 при 
; если 
наибольшая варианта, то 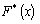= 1 при 
.
Эмпирическая функция распределения выборки является оценкой теоретической функции распределения генеральной совокупности.
ПРИМЕР 14.2.1. Дана выборка из генеральной совокупности объема N=100.
Таблица 14.2.4
| 254 | 1158 | 522 | 524 | 972 | 736 | 401 | 347 | 208 | 368 |
| 1485 | 812 | 1032 | 226 | 428 | 368 | 676 | 671 | 587 | 701 |
| 701 | 1171 | 443 | 683 | 786 | 895 | 267 | 597 | 51 | 941 |
| 659 | 400 | 484 | 876 | 570 | 241 | 678 | 127 | 728 | 903 |
| 424 | 245 | 531 | 986 | 1017 | 429 | 732 | 1021 | 430 | 153 |
| 513 | 520 | 221 | 1074 | 826 | 65 | 389 | 1180 | 504 | 325 |
| 294 | 447 | 1459 | 589 | 307 | 461 | 1434 | 559 | 837 | 743 |
| 382 | 387 | 967 | 446 | 763 | 767 | 349 | 853 | 578 | 652 |
| 285 | 628 | 688 | 517 | 380 | 375 | 878 | 409 | 109 | 621 |
| 712 | 476 | 432 | 721 | 1300 | 577 | 580 | 909 | 690 | 757 |
1) Находим из выборки и , рассчитываем размах выборки 
:
; 
; 
.
2) Составим вариационный ряд, для чего всю последовательность выборки расположим в порядке возрастания
| 51 | 65 | 109 | 127 | 153 | 208 | 221 | 226 | 241 | 245 |
| 254 | 267 | 285 | 294 | 307 | 325 | 347 | 349 | 368 | 368 |
| 375 | 380 | 382 | 387 | 389 | 400 | 401 | 409 | 424 | 428 |
| 429 | 430 | 432 | 443 | 446 | 447 | 461 | 476 | 484 | 504 |
| 513 | 517 | 520 | 522 | 524 | 531 | 559 | 570 | 577 | 578 |
| 580 | 587 | 589 | 597 | 621 | 628 | 652 | 659 | 671 | 676 |
| 678 | 683 | 688 | 690 | 701 | 701 | 712 | 721 | 728 | 732 |
| 736 | 743 | 757 | 763 | 767 | 786 | 812 | 826 | 837 | 853 |
| 876 | 878 | 895 | 903 | 909 | 941 | 967 | 972 | 986 | 1017 |
| 1021 | 1032 | 1074 | 1158 | 1171 | 1180 | 1300 | 1434 | 1459 | 1485 |
3) Задаем число 
количество частичных подынтервалов, на которое разбиваем нашу выборку : 
. Исходя из этого вычисляем длину подынтервалов 
и границы подынтервалов 
, 
;
;
;
;
;
;
;
;
.
4) Рассчитываем частоты – число попаданий в подынтервалы значений из выборки, то есть 
.
.
Контроль: 
.
На основе полученных данных, заполняем таблицу
| |
[51; 210,333) | [210,333; 369,666) | [369,666; 528,999) | [528,999; 688,332) | [688,332; 847,665) |
| |
6 | 14 | 25 | 18 | 16 |
| |
[847,665; 006,998) | [1006,998; 1166,331) | [1166,331; 1325,664) | [1325,664; 1485] |
| |
10 | 5 | 3 | 3 |
5) Считаем середины подынтервалов 
и относительные
частоты 
.
; 
;
.
Относительные частоты:
 |
 |
 |
 |
 |
 |
 |
 |
 |
Контроль:
.
В результате имеем таблицу:
Таблица 14.2.5
| |
130,6 | 290 | 449,3 | 608,6 | 768 | 927,3 | 1086,6 | 1246 | 1405 |
 |
0,06 | 0,14 | 0,25 | 0,18 | 0,16 | 0,1 | 0,05 | 0,03 | 0,03 |
6) Из данных табл. 14.2.5, получим эмпирический закон распределения относительных частот и визуальное его представление, то есть строим гистограмму и полигон распределения относительных частот.
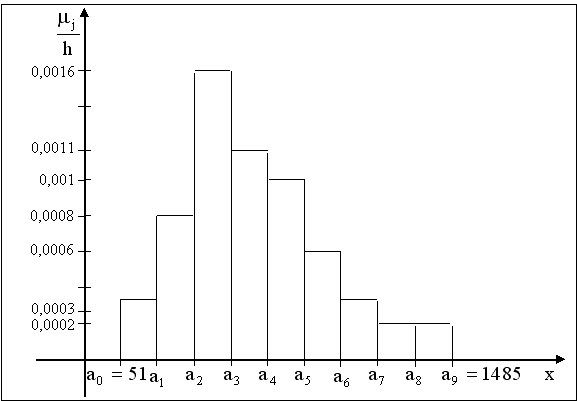
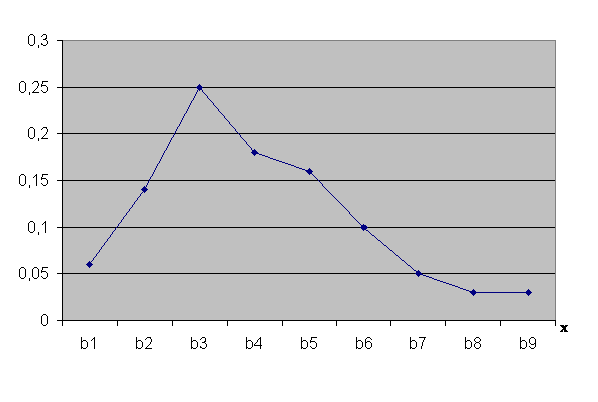
7) Составим эмпирическую функцию распределения. По определению, для группированного статистического ряда 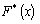, имеет вид
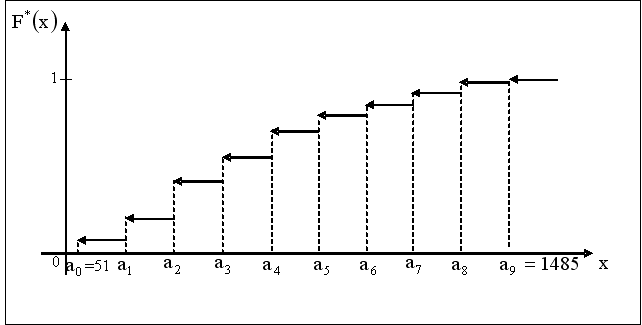
Построим график .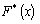
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
