Две случайные величины могут быть связаны между собой функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функциональная зависимость для случайных величин реализуется редко, так как обе величины (или одна из них) подвержены различным случайным факторам.
Пример 14.1.4. Рассмотрим две таблицы значений, которые принимают случайные величины 
и 
.
Таблица 14.1.6
| |
1 | 7 | 13 | 19 | 25 | 31 | 37 |
| |
15 | 3 | 25 | 2 | 10 | 16 | 8 |
Таблица 14.1.7
| |
1 | 7 | 13 | 19 | 25 | 31 | 37 |
| |
20 | 12 | 15 | 9 | 9 | 3 | 0 |
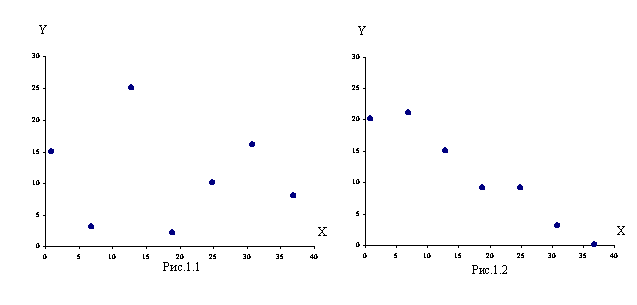
Изобразим эти данные в декартовой системе координат, откладывая значения случайной величины по оси 
, а значения случайной величины по оси 
.
Данные табл. 14.1.6 представлены на рис.1.1, данные табл. 14.1.7 – на рис.1.2. Из рис.1.1 видно, что данные табл. 14.1.6 не связаны между собой. А вот из рис.1.2 просматривается какая-то зависимость между и , причем выражена обратная зависимость: с увеличением значений случайной величины , значения случайной величины уменьшаются.
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. Если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной. Значит, корреляционная зависимость есть частный случай статистической зависимости.
Чтобы установить наличие и характер связи между двумя случайными величинами и , нужно привести к удобному виду исходный цифровой материал. Наглядной (удобной) формой представления данных является корреляционная таблица.
Таблица 14.1.8
 |
 |
 |
… |  |
… |  |
 |
 |
 |
 |
… |  |
… |  |
 |
 |
 |
 |
… |  |
… |  |
 |
| … | … | … | … | … | … | … | … |
 |
 |
 |
… |  |
… |  |
 |
| … | … | … | … | … | … | … | … |
 |
 |
 |
… |  |
… |  |
 |
 |
 |
 |
… |  |
… |  |
 |
Здесь 
; 
— середины подынтервалов сгруппированных выборок и (см. 14.1.2); — частота, с которой встречается пара 
. В последнем столбце и в последней строке таблицы помещены суммарные частоты, соответствующие значению 
, и соответственно 
, то есть
;
, тогда должно быть
и
.
— общее количество пар значений .
Каждая 
я строка табл. 14.1.8 представляет собой (совместно с первой строкой) некоторое распределение случайной величины , соответствующее данному значению случайной величины . Такое распределение называется условным распределением. Последняя строка табл. 14.1.8 совместно с первой строкой образует безусловное распределение случайной величины (ее эмпирический закон распределения):
Таблица 14.1.9
| |
|
|
… | |
… | |
| |
|
|
… | |
… | |
Каждый 
й столбец табл. 14.1.8 представляет собой совместно с первым столбцом некоторое распределение случайной величины , соответствующее данному значению случайной величины 
(то есть условное распределение). Последний столбец табл. 14.1.8 совместно с первым столбцом образует безусловное распределение случайной величины (ее эмпирический закон распределения):
Таблица 14.1.10
| |
|
|
… | |
… | |
| |
 |
 |
… | |
… | |
По данным табл. 14.1.9 и 14.1.10 вычисляем средние значения:
; 
(14.1.15)
и средние квадратические отклонения:
; 
. (14.1.16)
Замечание 14.1.3. Рекомендуется сделать два рисунка – это графические изображения эмпирических законов распределения случайных величин и в виде распределения частот. На рисунках нанести средние значения 
и 
.
Уточним определение корреляционной зависимости. Для этого введем понятие условной средней. Для каждой 
-й строки табл. 14.1.8 (совместно с первой строкой) можно вычислить среднее значение случайной величины (по формуле 14.1.15), которое называется условным средним:
.
Так как каждому значению соответствует одно значение условной средней, то, очевидно, условная средняя 
есть функция от . В этом случае говорят, что случайная величина зависит от корреляционно.
Корреляционной зависимостью от называют функциональную зависимость условной средней 
от :
. (14.1.17)
Уравнение (14.1.17) называется уравнением регрессии на ; функция 
называется регрессией на ; график функции — линией регрессии на .
Аналогично для каждого го столбца табл. 14.1.8 (совместно с первым столбцом) можно вычислить среднее значение случайной величины по формуле (14.1.15), которое называется условным средним:
.
Тогда корреляционной зависимостью от называется функциональная зависимость 
от :
. (14.1.18)
Уравнение (14.1.18) называется уравнением регрессии на ; функция 
называется регрессией на ; график функции — линией регрессии на .
Замечание 14.1.4. Рассматриваемые два уравнения регрессии существенно различны и не могут быть получены одно из другого.
Изучение корреляционной связи будем проводить при решении двух основных задач:
— определение формы корреляционной связи, то есть вида теоретической функции регрессии (она может быть линейной и нелинейной);
— определение тесноты (силы) корреляционной связи.
Наиболее простой и важный случай корреляционной зависимости — линейная регрессия. В этом случае теоретическое уравнение линейной регрессии на (формула 14.1.17) имеет вид
. (14.1.19)
Коэффициент 
в уравнении (14.1.19) называют коэффициентом регрессии на и обозначают 
. Оценки неизвестных параметров 
и 
рассчитаем, применяя данные табл. 14.1.8:
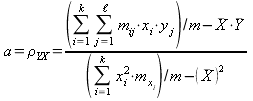. (14.1.20)
, (14.1.21)
где и — средние значения случайных величин и , вычисленные по формулам (14.1.15).
Сделаем графическое изображение так называемой эмпирической линии регрессии на и теоретической линии регрессии на . Для этого в декартовой системе координат по оси откладываем значения из табл. 14.1.8, по оси откладываем значения условных средних . Тогда ломаная линия, соединяющая точка 
; 
; … ; 
, и будет эмпирической линией регрессии на . Здесь же на данном графике строим теоретическую линию регрессии, то есть прямую 
с вычисленными коэффициентами.
Замечание 14.1.5. Поскольку формулы (14.1.20) и (14.1.21) получены по методу наименьших квадратов, то по сути этого метода, теоретическая линия регрессии должна на графике быть в «середине» ломаной.
Аналогично можно поставить вопрос о нахождении теоретического уравнения линейной регрессии на (формула 14.1.18), которое в этом случае имеет вид
. (14.1.22)
Коэффициент 
в уравнении (14.1.22) называют коэффициентом регрессии на и обозначают 
. Оценки неизвестных параметров 
и 
рассчитываются по данным табл.1.8:
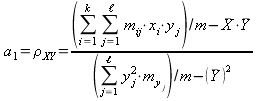. (14.1.23)
, (14.1.24)
где и средние значения случайных величин и , вычисленные по формулам (14.1.15).
Далее целесообразно сделать графическое изображение эмпирической и теоретической линий регрессии на аналогично вышеизложенному.
В случае линейной регрессии задача определения тесноты связи сводится к вычислению эмпирического (выборочного) коэффициента корреляции, который можно вычислить по одной из формул:
или 
, (14.1.25)
где 
— значения средних квадратических отклонений, вычисленных по формуле (14.1.16).
Приведем свойства выборочного коэффициента корреляции:
1. 
или 
.
2. Если 
, тогда и 
не связаны линейной корреляционной зависимостью (но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью).
3. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при 
переходит в линейную функциональную зависимость.
4. Если 
, тогда и связаны прямой (обратной) линейной функциональной зависимостью.
Замечание 14.1.6. Однако эмпирический коэффициент корреляции является весьма условным показателем даже линейной связи, так как он является средней пропорциональной величиной между коэффициентами регрессии. В теории корреляции существует понятие корреляционного отношения, которое является более естественным и общим показателем степени тесноты связи, так как не связано с формой зависимости.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >