Все дифференциальные уравнения порядка выше первого называют дифференциальными уравнениями высших порядков. Как мы уже знаем, порядком дифференциального уравнения называют порядок старшей производной, входящей в состав уравнения; таким образом, можно дать следующее определение – определение дифференциального уравнения 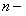 порядка.
порядка.
ОПРЕДЕЛЕНИЕ 11.1.11 Дифференциальными уравнениями 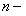 порядка называются уравнения, связывающие независимую переменную, функцию и производные (или дифференциалы) этой функции до
порядка называются уравнения, связывающие независимую переменную, функцию и производные (или дифференциалы) этой функции до 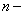 го порядка включительно.
го порядка включительно.
Его общий вид
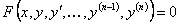
или, предполагая уравнение разрешенным относительно старшей производной,
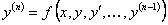 (11.1.15)
(11.1.15)
Функция 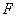 или
или 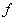 может и не зависеть от некоторых из аргументов x,y
может и не зависеть от некоторых из аргументов x,y 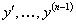 , но во всех случаях уравнение
, но во всех случаях уравнение 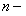 го порядка должно содержать производную
го порядка должно содержать производную 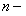 го порядка.
го порядка.
ОПРЕДЕЛЕНИЕ 11.1.12 Решением дифференциального уравнения (11.1.15) называется всякая функция 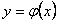 , которая удовлетворяет этому уравнению, то есть
, которая удовлетворяет этому уравнению, то есть
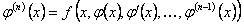 .
.
Решение уравнения (11.1.15) может быть задано также в неявном виде: 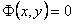 . График решения уравнения (11.1.15) называется интегральной кривой.
. График решения уравнения (11.1.15) называется интегральной кривой.
Задача Коши для уравнения ставится так. Найти решение уравнения (11.1.15), удовлетворяющее начальным условиям
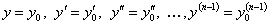 при
при 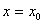 (11.1.16)
(11.1.16)
где 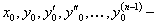 заданные числа.
заданные числа.
В случае уравнения второго порядка 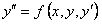 начальные условия имеют вид
начальные условия имеют вид 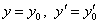 при
при 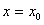 , то есть в точке
, то есть в точке 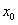 задаются значения искомой функции
задаются значения искомой функции 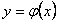 к ее первой производной
к ее первой производной 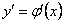 . Геометрически в задаче Коши речь идет о нахождении интегральной кривой
. Геометрически в задаче Коши речь идет о нахождении интегральной кривой 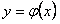 , проходящей через заданную точку
, проходящей через заданную точку 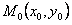 и имеющей в этой точке заданный наклон касательной
и имеющей в этой точке заданный наклон касательной 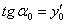 (рис. 11.5).
(рис. 11.5).
Возникает вопрос: можно ли по виду правой части уравнения
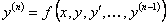
сказать, имеет ли оно решение, удовлетворяющее начальным условиям (11.1.16), и будет ли это решение единственным? Ответ на этот вопрос дает следующая теорема существования и единственности решения.
ТЕОРЕМА 11.1.4 Если в уравнении (1) функция 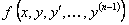 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) она непрерывна по всем своим аргументам 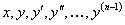 в некоторой области
в некоторой области 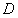 их изменения;
их изменения;
2) существуют частные производные 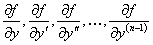 в области
в области 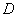 и они ограничены
и они ограничены 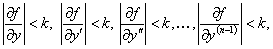 то уравнение (11.1.15) имеет единственное решение
то уравнение (11.1.15) имеет единственное решение 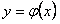 , удовлетворяющее начальным условиям (11.1.16).
, удовлетворяющее начальным условиям (11.1.16).
ПРИМЕР 11.1.19 Для уравнения 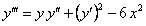 существует единственное решение, удовлетворяющее начальным условиям
существует единственное решение, удовлетворяющее начальным условиям 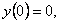
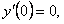
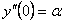 . Таким решением будет
. Таким решением будет 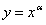 . Других решений, удовлетворяющих этим начальным условиям, нет.
. Других решений, удовлетворяющих этим начальным условиям, нет.
ОПРЕДЕЛЕНИЕ 11.1.13 Функция
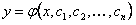 (11.1.17)
(11.1.17)
называется общим решением уравнения (1) в некоторой области 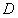 изменения переменных
изменения переменных 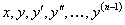 , если она удовлетворяет условиям:
, если она удовлетворяет условиям:
1) система уравнений
 (11.1.18)
(11.1.18)
разрешима в области 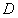 относительно произвольных постоянных
относительно произвольных постоянных 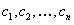 , так что мы имеем
, так что мы имеем

2) функция (11.1.17) является решением дифференциального уравнения при всех значениях произвольных постоянных.
Всякое решение, получающееся из общего решения (11.1.17) при конкретных числовых значениях произвольных постоянных 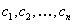 , называется частным решением.
, называется частным решением.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >