Для теории вероятностей характерно то, что результаты рассматриваемых экспериментов можно представить числом, причем случайный характер исхода влечет и случайность этого числа.
Случайной величиной называется величина, которая в результате опыта может принять какое-либо числовое значение, заранее нам не известное.
Как видно из примеров по типу множества возможных значений случайные величины бывают дискретные, непрерывные и кусочно-непрерывные.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого промежутка.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
Существует универсальный способ задания закона распределения, который годится для случайных величин любого типа: функцией распределения случайной величины X называется функция F(X), равная вероятности того, что X примет значение меньше, чем число x,то есть 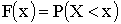 . Иногда ее называют интегральной функцией распределения.
. Иногда ее называют интегральной функцией распределения.
Из определения следует: 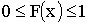 и
и 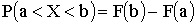 .
.
Непрерывную случайную величину можно также задать, используя другую функцию f(X)=F'(X), которую называют плотностью распределения вероятностей (иногда ее называют дифференциальной функцией).
Из определения следует:
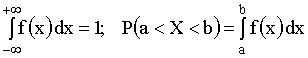 .
.
Одна из числовых характеристик, фиксирующая положение случайной величины на числовой оси, то есть некоторое среднее, ориентировочное значение случайной величины, около которого группируются ее возможные значения – математическое ожидание M(X).
Математическое ожидание вычисляется:
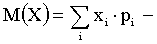 для дискретной случайной величины;
для дискретной случайной величины;
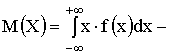 для непрерывной случайной величины.
для непрерывной случайной величины.
Дисперсия D(X) — есть характеристика рассеяния, разбросанности случайной величины около ее математического ожидания.
Дисперсия вычисляется:
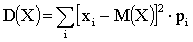 для дискретной случайной величины;
для дискретной случайной величины;
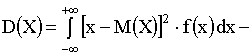 для непрерывной случайной величины.
для непрерывной случайной величины.
Иногда дисперсию удобно вычислять по следующей формуле:
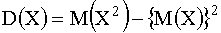 .
.
Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому вводится еще одна характеристика рассеяния – среднее квадратическое отклонение 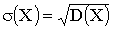 .
.
Математическое ожидание обладает следующими свойствами:
1.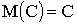 , где
, где 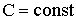 ;
;
2.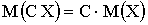 , где
, где 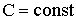 ;
;
3. 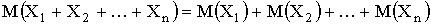 ;
;
4. 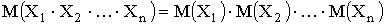 , если
, если 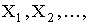
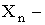 взаимно независимые случайные величины.
взаимно независимые случайные величины.
Дисперсия обладает следующими свойствами:
1.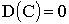 , где
, где 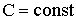 ;
;
2.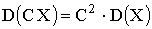 , где
, где 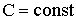 ;
;
3.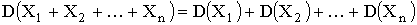 , если
, если 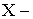
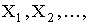
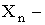 независимые случайные величины.
независимые случайные величины.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.36. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 10 рублей. Написать закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: 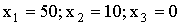 . Вероятности этих возможных значений таковы:
. Вероятности этих возможных значений таковы:
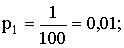 ,
,
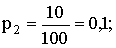 ,
,
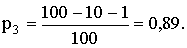 .
.
Напишем искомый закон распределения
| X | 50 | 10 | 0 |
| P | 0,01 | 0,1 | 0,89 |
Контроль: 0,01+0,1+0,89=1.
ПРИМЕР 13.2.37. Функция распределения непрерывной случайной величины X задана выражением: 
Найти: а) коэффициент a; б) найти плотность распределения f(X); в) найти вероятность того, что случайная величина X в результате опыта примет значение между 0,25 и 0,5.
Решение. а) Для непрерывной случайной величины функция F(x) непрерывна, следовательно, 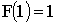 , то есть
, то есть 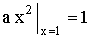 , откуда
, откуда 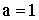 .
.
б) Плотность распределения 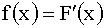 выражается формулой:
выражается формулой:

в) Воспользуемся формулой 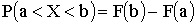 . Тогда,
. Тогда,
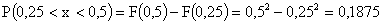 .
.
ПРИМЕР 13.2.38. Дискретная случайная величина X задана законом распределения
| X | 4 | 6 | 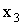 |
| P | 0,5 | 0,3 | 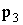 |
Найти: а) 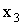 и
и 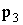 , зная, что
, зная, что 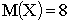 ; б) дисперсию D(X).
; б) дисперсию D(X).
Решение. а) Известно, что 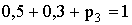 . Тогда
. Тогда 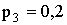 . По определению математического ожидания
. По определению математического ожидания 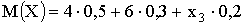 ;
; 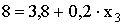 ;
; 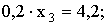 ,
, 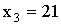 .
.
Закон распределения будет иметь вид:
| X | 4 | 6 | 21 |
| P | 0,5 | 0,3 | 0,2 |
б) Дисперсию можно вычислить двумя способами:
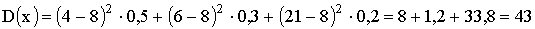 .
.
Для второго способа напишем закон распределения случайной величины 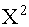 :
:
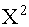 |
16 | 36 | 441 |
| P | 0,5 | 0,3 | 0,2 |
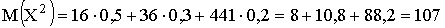 ,
,
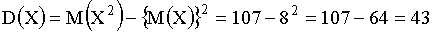 .
.
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулы расчета вероятности для случайных величин
3.2.7.1. В урне 5 белых и 25 черных шаров. Вынули наугад 1 шар. Случайная величина X — число вынутых белых шаров.
Требуется:
а) построить ряд распределения СВ X;
б) построить функцию распределения СВ X;
в) найти M(X) и D(X).
Отв.:
a)
| X | 0 | 1 |
| P | 5/6 | 1/6 |
б)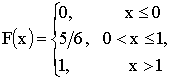 , в)
, в)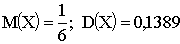 .
.
3.2.7.2. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных. Найти M(X), D(X).
Отв.: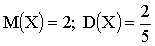
3.2.7.3. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов таковы: 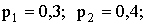 ,
, 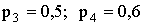 . Найти M(X), D(X) и среднее квадратическое отклонение СВ X — числа отказавших приборов.
. Найти M(X), D(X) и среднее квадратическое отклонение СВ X — числа отказавших приборов.
Отв.:1,8; 0,94; 0,97
3.2.7.4. Случайная величина X — может принимать два возможных значения: 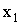 с вероятностью 0,3 и
с вероятностью 0,3 и 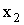 с вероятностью 0,7; причем
с вероятностью 0,7; причем 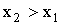 . Найти
. Найти 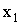 и
и 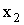 , зная, что
, зная, что 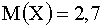 и
и 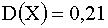 .
.
Отв.: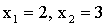
3.2.7.5. Дан перечень возможных значений дискретной случайной величины X : 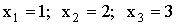 , а также известно, что
, а также известно, что 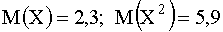 . Найти вероятности, соответствующие возможным значениям X.
. Найти вероятности, соответствующие возможным значениям X.
Отв.:
3.2.7.6. Даны независимые случайные величины X и Y.
| X | -1 | 0 | 1 | Y | 2 | 4 | |
| P | 0,2 | 0,5 | 0,3 | P | 0,3 | 0,7 |
Найти математическое ожидание и дисперсию следующих случайных величин: а)X+Y; б)2X-3Y ; в)X-Y+5 .
Отв.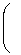
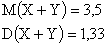
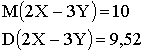
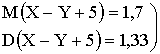 :
:
3.2.7.7. Брошены n игральных костей. Случайная величина X — сумма числа очков, которые выпадут на всех гранях. Найти: а) M(X); б) D(X).
Отв.: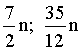
3.2.7.8. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равно 0,9. Найти M(X) дискретной случайной величины X — числа партий, в каждой из которых окажется ровно четыре стандартных изделия, если проверке подлежит 50 партий.
Отв.: 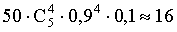
3.2.7.9. Вероятность того, что в обувном магазине есть обувь, подходящей для покупателя модели, равна 0,6, а вероятность наличия обуви подходящего размера равна 0,8. Построить функцию распределения случайной величины X – числа обувных магазинов, которые посетит покупатель, если в городе три магазина.
Отв.:
| X | 1 | 2 | 3 |
| P | 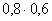 |
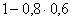 |
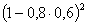 |
3.2.7.10. Имеется 6 ключей, из которых только один подходит к замку. Найти закон распределения случайной величины Х — числа попыток при открывании замка, если испробованный ключ в последующих попытках не участвует. Найти M(X) и 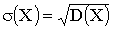 .
.
Отв.:
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 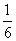 |
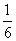 |
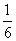 |
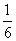 |
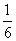 |
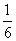 |
M(X)=3,5;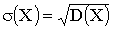 =
=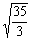
3.2.7.11. Два баскетболиста независимо друг от друга делают по одному броску в одну корзину. Вероятность попадания при одном броске равна 0,6 и 0,9 соответственно. Найти закон распределения случайной величины Х – числа попаданий в корзину. Найти M(X) и D(X).
Отв.:
| X | 0 | 1 | 2 |
| P | 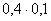 |
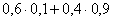 |
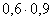 |
M(X)=1,5;D(X)=1,08
3.2.7.12. Вероятность того, что на АЗС есть в наличии бензин марки Аи-95, необходимый автомобилисту, равна 0,9. Построить функцию распределения случайной величины X – числа АЗС, которые посетит автомобилист, если в городе пять АЗС. Найти M(X), D(X).
Отв.:
| X | 1 | 2 | 3 | 4 | 5 |
| P | 0,9 | 0,09 | 0,009 | 0,0009 | 0,00001 |
M(X)=1,1111;D(X)=0,123
3.2.7.13. Случайная величина X — задана функцией распределения 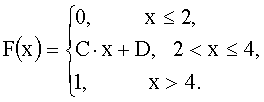
Найти:
а) параметры C и D;
б) плотность распределения f(x) ;
в) 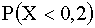 ;
;
г) 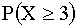 ;
;
д) 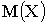 ;
;
е) M(X); ж) D(X).
Отв.: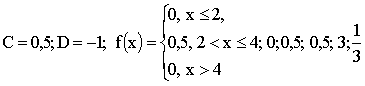
3.2.7.14. Случайная величина задана функцией распределения 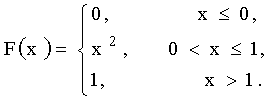
Найти вероятность того, что в результате четырех независимых испытаний величина X — ровно три раза примет значение, принадлежащее интервалу (1/4; 3/4).
Отв.:0,25
3.2.7.15. Плотность распределения непрерывной случайной величины X задана на всей оси Ox функцией
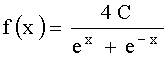 .
.
Найти постоянный параметр C.
Отв.: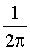
3.2.7.16. Случайная величина X — задана плотностью распределения 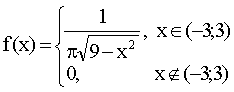
Найти: а) математическое ожидание и дисперсию СВ X; б) установить, что вероятнее: в результате испытания окажется X < 1 или X > 1.
Отв.: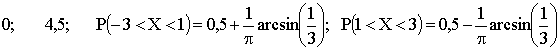
3.2.7.17. Функция распределения случайной величины X — задана формулой 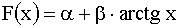 . Найти: а) постоянные
. Найти: а) постоянные 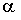 и
и 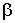 ; б) плотность распределения; в) вероятность того, что СВ X попадет на отрезок [-1;1] ; г)математическое ожидание и дисперсию СВ X.
; б) плотность распределения; в) вероятность того, что СВ X попадет на отрезок [-1;1] ; г)математическое ожидание и дисперсию СВ X.
Отв.: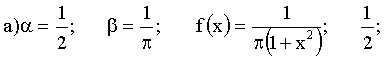 математическое ожидание не существует, а дисперсия бесконечна;
математическое ожидание не существует, а дисперсия бесконечна;
3.2.7.18. Случайная величина X имеет плотность распределения 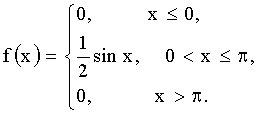
Требуется а) Построить функцию распределения F(X).
б) Найти вероятность того, что в результате испытания 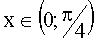 .
.
Отв.: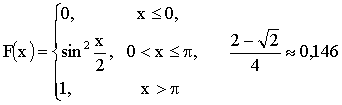
3.2.7.19. Среднее квадратическое отклонение каждой из 16 одинаково распределенных взаимно независимых случайных величин равно 10. Найти среднее квадратическое отклонение среднего арифметического этих величин.
Отв.:2,5
Онлайн помощь по математике
Лекции по высшей математике
Примеры решения задач