Как любая наука, теория вероятностей имеет свои исходные понятия, через которые определяются другие понятия. К основным понятиям теории вероятностей относятся: испытание, событие, вероятность события.
Изучение явлений происходит путем наблюдений и опытов, проводимых при определенных условиях. Испытанием в теории вероятностей называется осуществление какого-либо комплекса условий, при котором наблюдается данное явление. Предполагается, что данный комплекс условий может быть воспроизведен сколь угодно большое число раз. Итак, в теории вероятностей вместо слов “произведено наблюдение при осуществлении определенного комплекса условий” говорят кратко “произведено испытание”.
Событием называется всякий факт, который может наступить в результате испытания.
Примеры:
- бросание монеты — испытание, выпадение герба – событие;
- стрельба по цели – испытание, промах – событие;
- бросание игральной кости – испытание, выпало пять очков – событие.
События можно классифицировать по степени возможности их появления и по характеру взаимосвязи.
Достоверным называется событие, которое в данном испытании всегда наступает, его обозначают 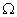 .
.
Невозможным называется событие, которое в данном испытании никогда не наступает, его обозначают 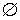 .
.
Случайным называется событие, которое в данном испытании может наступить, а может не наступить. Случайные события обозначают заглавными буквами латинского алфавита А, В, С,…
Примеры:
- В урне три белых и пять красных шаров. Из урны наугад извлекается один шар – испытание.
- А={шар красный} – случайное;
- B ={шар синий} – невозможное;
- C ={шар красный или белый} – достоверное.
- По цели произведен пуск двух ракет – испытание.
- A = {попадание в цель не более двух ракет} – достоверное;
- B= { попадание в цель трех ракет} – невозможное;
- C = {одно попадание в цель} – случайное.
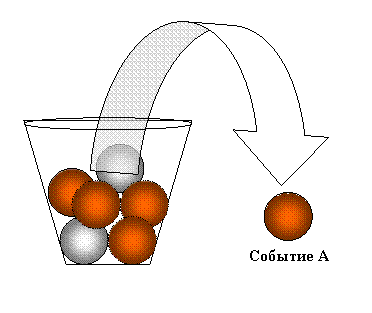 .
.
События:
События:
События называются несовместными, если появление одного из них исключает появление других событий в данном испытании. В противном случае события называются совместными. Примеры несовместных событий: появление герба и цифры при одном бросании монеты, попадание и промах при одном выстреле. Те же попадание и промах при двух выстрелах являются уже совместными событиями.
Несколько событий образуют полную группу событий, если в результате испытания обязательно наступит хотя бы одно из них. В частности, если события образуют полную группу и несовместны, то в результате испытания появится одно и только одно из этих событий.
Суммой событий 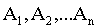 . называется событие, состоящее в наступлении хотя бы одного из этих событий.
. называется событие, состоящее в наступлении хотя бы одного из этих событий.
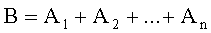 .
.
Произведением событий его обозначают 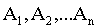 . называется событие, состоящее в совместном появлении всех этих событий.
. называется событие, состоящее в совместном появлении всех этих событий.
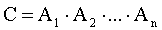 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >