Дано дифференциальное уравнение
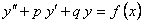 ,(11.1.41)
,(11.1.41)
где 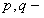 действительные числа.
действительные числа.
В предыдущих параграфах был дан общий метод нахождения общего решения неоднородного дифференциального уравнения. В этом параграфе покажем нахождение частных решений линейного дифференциального уравнения второго порядка с постоянными коэффициентами
1.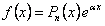 ,(11.1.42)
,(11.1.42)
где 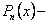 многочлен
многочлен 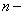 ой степени,
ой степени, 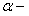 постоянная.
постоянная.
Тогда возможны следующие случаи:
а) Число 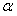 не является корнем характеристического уравнения
не является корнем характеристического уравнения
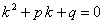 .
.
В этом случае частное решение нужно искать в виде
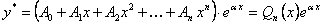 , (11.1.43)
, (11.1.43)
где 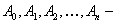 коэффициенты, подлежащие определению.
коэффициенты, подлежащие определению.
Подставляя 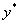 в уравнение (11.1.41) и сокращая все члены на множитель
в уравнение (11.1.41) и сокращая все члены на множитель 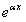 , имеем
, имеем
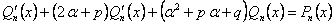 .(11.1.44)
.(11.1.44)
Слева и справа от знака равенства стоит многочлен 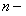 й степени, приравнивая коэффициенты при одинаковых степенях
й степени, приравнивая коэффициенты при одинаковых степенях 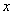 , получим систему
, получим систему 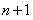 уравнений для определения неизвестных коэффициентов
уравнений для определения неизвестных коэффициентов 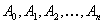 .
.
б) Число 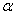 есть простой корень характеристического уравнения. В этом случае частное решение нужно искать в виде
есть простой корень характеристического уравнения. В этом случае частное решение нужно искать в виде
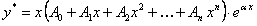 .
.
Неизвестные коэффициенты 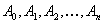 определяем так же как в пункте а.
определяем так же как в пункте а.
в) Число 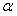 двукратный корень характеристического уравнения. Тогда частное решение
двукратный корень характеристического уравнения. Тогда частное решение 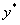 следует искать в виде
следует искать в виде
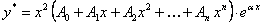 .
.
Неизвестные коэффициенты 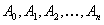 определяем так же как в пункте а.
определяем так же как в пункте а.
2. Правая часть уравнения (11.1.41) имеет вид
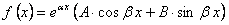 , где
, где 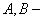 постоянные.
постоянные.
а) Если число 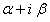 не является корнем характеристического уравнения, то частное
не является корнем характеристического уравнения, то частное 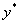 следует искать в виде
следует искать в виде
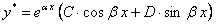 , где
, где 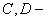 числа, подлежащие определению.
числа, подлежащие определению.
б) Если число 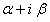 является корнем характеристического уравнения, то частное решение следует искать в виде
является корнем характеристического уравнения, то частное решение следует искать в виде
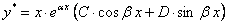 .
.
ПРИМЕР 11.1.28 Найти общее решение дифференциального уравнения 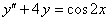 .
.
Решение.
Составляем характеристическое уравнение 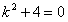 , которое имеет корни
, которое имеет корни 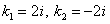 , поэтому общее решение соответствующего однородного уравнения имеет вид
, поэтому общее решение соответствующего однородного уравнения имеет вид 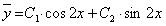 .
.
Для этого случая 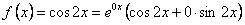 ,
, 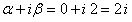 . Это число является корнем характеристического уравнения, поэтому частное решение
. Это число является корнем характеристического уравнения, поэтому частное решение 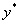 неоднородного находим в виде
неоднородного находим в виде
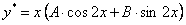 . Подставляя
. Подставляя 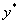 в дифференциальное уравнение и приравнивая коэффициенты при
в дифференциальное уравнение и приравнивая коэффициенты при 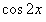 и
и 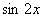 , получаем систему уравнений для определения
, получаем систему уравнений для определения 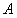 и
и 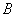 :
: 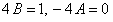 , откуда
, откуда 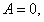
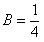 .
.
Тогда общее решение данного дифференциального уравнения имеет вид 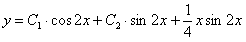 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >