Линейно-зависимые и независимые функции. Определитель Вронского

Даны непрерывные функции 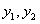на интервале .

ОПРЕДЕЛЕНИЕ 11.1.15 Функции 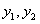называются линейно-независимыми на интервале , если их отношение на этом отрезке не является постоянным, то есть 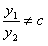. В противном случае функции называются линейно зависимыми.

ПРИМЕР 11.1.23 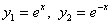. Проверить линейную независимость этих функций.

Решение.

Согласно определению найдем .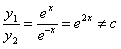

Отсюда следует, что функции 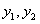линейно независимы.

Помощь с решением задач

ОПРЕДЕЛЕНИЕ 11.1.16 Определителем Вронского для функций 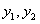называется определитель вида .

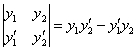Определитель Вронского для функций 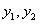обозначают через .

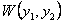ТЕОРЕМА 11.1.8 Если функции 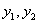линейно зависимы на интервале , то определитель Вронского для этих функций на этом интервале тождественно равен нулю.

Доказательство. По условию теоремы функции линейно зависимы, согласно определению 1 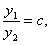то есть 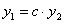. Тогда

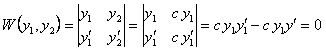Теперь рассмотрим случай, когда функции 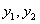являются решениями уравнения

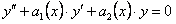.(11.1.20)

ТЕОРЕМА 11.1.9 Если определитель Вронского 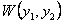составленный для решений 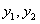линейного дифференциального уравнения (11.1.20), не равен нулю при каком-нибудь значении 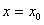на интервале , то он не обращается в нуль ни при каком значении 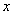на этом интервале.

Доказательство. По условию 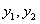являются решениями уравнения (11.1.20), то выполняются равенства

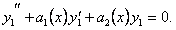(11.1.21)

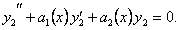(11.1.22)

Умножая обе части равенства (11.1.21) на 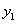, обе части равенства (11.1.22) на 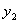и вычитая полученные равенства, имеем:

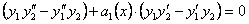.(11.1.23)

Разность, заключенная во вторую скобку, есть определитель Вронского 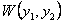. Разность, заключенная в первую скобку, есть производная от определителя Вронского

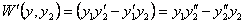
Следовательно равенство (11.1.23) принимает вид

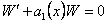(11.1.24)

Найдем решение дифференциального уравнения (11.1.24), удовлетворяющее начальному условию

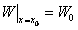.(11.1.25)

Разделяя переменные в уравнении (11.1.24), получаем .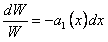

Интегрируя, находим 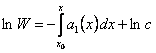или

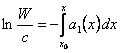. Откуда

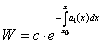.(11.1.26)

Найдем 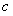так, чтобы удовлетворялось начальное условие (11.1.25). Подставляя 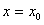в левую и правую часть равенства (11.1.26), получаем .

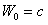Тогда решением уравнения (11.1.24), удовлетворяющее начальным условиям (11.1.25) принимает вид:

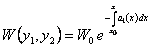По условию 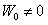, тогда из последнего равенства следует, что 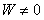ни при каком значении 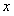, так как показательная функция не обращается в нуль ни при каком значении аргумента .

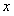ТЕОРЕМА 11.1.10 Если решения 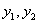уравнения (11.1.20) линейно независимы на интервале , то определитель Вронского 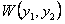, составленный для этих решений, не обращается в нуль ни в одной точке интервала .

Доказательство. Допустим, что 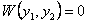в некоторой точке интервала . Тогда по теореме 11.9 определитель Вронского 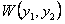будет равен нулю во всех точках интервала .

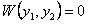или .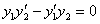

Допустим, что 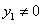на интервале . Тогда на основании последнего равенства можно написать 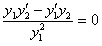или .

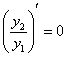Откуда следует 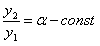, то есть решения 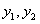линейно зависимы, что противоречит условию теоремы о их линейной зависимости.

Допустим, что 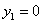в точках принадлежащих интервалу . Рассмотрим интервал 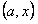. На этом интервале 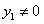. Следовательно, на основании только что доказанного следует, что на интервале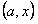 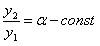или .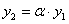

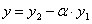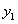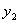Рассмотрим функцию . Так как и являются решениями уравнения (11.1.21), то 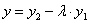есть так же решение уравнения (11.1.20) и удовлетворяют условию .

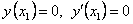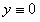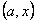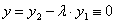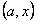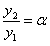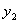Из теоремы существования и единственности решения задачи Коши следует, что на интервале . Отсюда следует, что на интервале или на интервале , то есть и 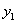линейно зависимы, что противоречит условию теоремы о линейной независимости решени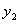й и 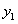. Тем самым доказано, что определитель Вронского не обращается в нуль ни в одной из точек интервала .