ОПРЕДЕЛЕНИЕ 11.2.17 Уравнение вида
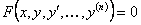 (11.2.10)
(11.2.10)
называется дифференциальным уравнением 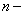 го порядка.
го порядка.
ОПРЕДЕЛЕНИЕ 11.2.18 Всякая 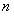 раз дифференцируемая функция
раз дифференцируемая функция 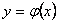 , которое обращает уравнение (11.2.10) в тождество называется решением уравнения (11.2.10).
, которое обращает уравнение (11.2.10) в тождество называется решением уравнения (11.2.10).
Задача Коши для уравнения (11.2.10) состоит в том, чтобы найти решение уравнения, удовлетворяющее условиям 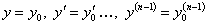 при
при 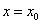 , где
, где 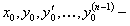 начальные условия.
начальные условия.
ОПРЕДЕЛЕНИЕ 11.2.19 Функция 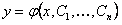 называется общим решением уравнения (11.2.10), если при соответствующем выборе произвольных постоянных
называется общим решением уравнения (11.2.10), если при соответствующем выборе произвольных постоянных 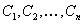 эта функция является решением любой задачи Коши, поставленной для данного уравнения.
эта функция является решением любой задачи Коши, поставленной для данного уравнения.
Одним из основных методов, применяемых при интегрировании дифференциальных уравнений высших порядков, является понижение порядка уравнения, т.е. сведение уравнения путем замены к уравнению, порядка которого ниже данного.
Понижение порядка возможно не для всякого уравнения, в связи с чем представляют интерес некоторые типы неполных дифференциальных уравнений, допускающих понижение порядка.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >