В данном параграфе речь пойдет о линейных неоднородных дифференциальных уравнениях n-го порядка с постоянными коэффициентами вида
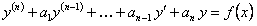 .(11.2.13)
.(11.2.13)
ОПРЕДЕЛЕНИЕ 11.2.23 Если функция правой части 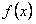 не тождественный нуль, такие уравнения называют неоднородными или уравнениями с правой частью.
не тождественный нуль, такие уравнения называют неоднородными или уравнениями с правой частью.
Коэффициенты 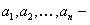 известные константы (в данном параграфе это замечание не принципиально – все выкладки имеют место и в случае зависящих от
известные константы (в данном параграфе это замечание не принципиально – все выкладки имеют место и в случае зависящих от 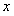 коэффициентов).
коэффициентов).
Общее решение уравнения (11.2.13) представляет собой сумму
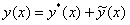 , (11.2.14)
, (11.2.14)
где 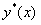 — какое-либо частное решение неоднородного уравнения,
— какое-либо частное решение неоднородного уравнения, 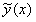 — общее решение однородного уравнения при
— общее решение однородного уравнения при 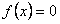 .
.
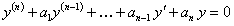 . (11.2.15)
. (11.2.15)
Пусть фундаментальная система решений однородного уравнения известна: 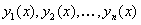 . Тогда общее решение однородного уравнения можно выписать
. Тогда общее решение однородного уравнения можно выписать 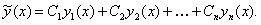 Таким образом, для построения общего решения необходимо найти какое-либо частное решение
Таким образом, для построения общего решения необходимо найти какое-либо частное решение 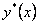 .
.
Для нахождения частного решения неоднородного уравнения можно пользоваться методом вариации произвольных постоянных. Он заключается в следующем. Решение уравнения (11.2.13) находится в виде линейной комбинации функций 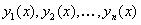 с коэффициентами, уже зависящими от
с коэффициентами, уже зависящими от 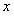 :
:
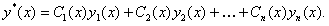
Производные от функций 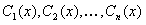 определяются из линейной алгебраической системы вида
определяются из линейной алгебраической системы вида
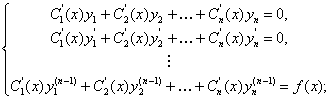 (11.2.16)
(11.2.16)
где f(x) – правая часть уравнения (11.2.13). Вывод этой формулы можно найти в учебниках.
Определитель системы равен вронскиану 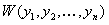 и в нуль не обращается. Это обеспечивает однозначную разрешимость системы. Тем или иным методом линейной алгебры можно получить выражения для
и в нуль не обращается. Это обеспечивает однозначную разрешимость системы. Тем или иным методом линейной алгебры можно получить выражения для 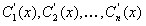 ; сами функции восстанавливаются интегрированием. В частности для дифференциального уравнения второго порядка система имеет вид.
; сами функции восстанавливаются интегрированием. В частности для дифференциального уравнения второго порядка система имеет вид.
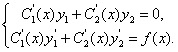 (11.2.17)
(11.2.17)
Неизвестные 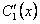 и
и 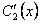 определяются по формулам Крамера
определяются по формулам Крамера
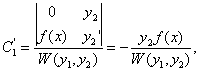
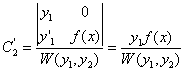 ,
,
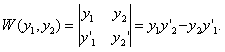 (11.2.18)
(11.2.18)
Решения выписываются через интегралы
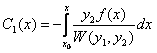 ,
, 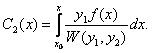 (11.2.19)
(11.2.19)
ПРИМЕР 11.2.116 Найти общее решение уравнения 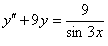 .
.
Решение.
Общее решение по теореме о структуре решений, имеет вид 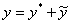 .
. 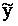 находим при решении однородного уравнения
находим при решении однородного уравнения 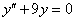 . Составим характеристическое уравнение
. Составим характеристическое уравнение 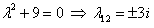 общее решение однородного уравнения будет иметь вид
общее решение однородного уравнения будет иметь вид  , где
, где 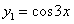 и
и 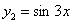 . Частное решение данного уравнения по методу вариации будет иметь вид
. Частное решение данного уравнения по методу вариации будет иметь вид 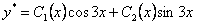 .
.
Составим систему 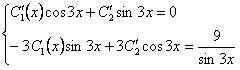 .
.
Вычислим главный определитель системы
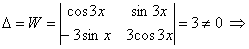 система имеет единственное решение, по формулам Крамера имеем
система имеет единственное решение, по формулам Крамера имеем
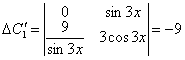 ;
; 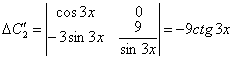 .
.
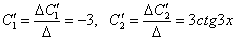 . Интегрируя последнее равенство, найдем
. Интегрируя последнее равенство, найдем 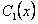 и
и 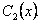
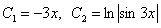 .
.
Запишем частное решение неоднородного уравнения 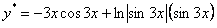 , тогда общее решение будет иметь вид
, тогда общее решение будет иметь вид 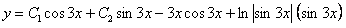 .
.
Задачи и примеры для самостоятельного решения
Найти общее решение дифференциальных уравнений
11.2.117 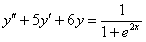 .
.
Отв. 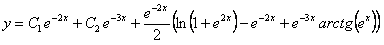
11.2.118 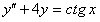 .
.
Отв. 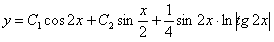 .
.
11.2.119 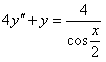 .
.
Отв. 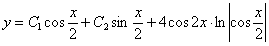 .
.
11.2.120 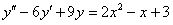 .
.
Отв. 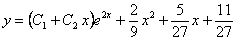 .
.
11.2.121 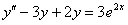 .
.
Отв. 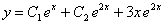 .
.
11.2.122 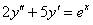 .
.
Отв. 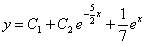 .
.
11.2.123 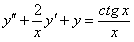 .
.
Отв. 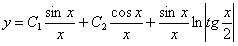 .
.
11.2.124 Найти решение уравнения 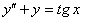 , удовлетворяющее краевым условиям
, удовлетворяющее краевым условиям 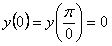 .
.
Отв. 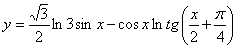 .
.
Замечание. Краевые условия – это условия заданные на концах некоторого промежутка, их число не должно превышать порядка уравнения.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >