ОПРЕДЕЛЕНИЕ 12.2.5 Выражение 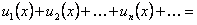
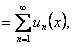 где
где 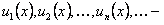 функции, заданные на одном и том же множестве
функции, заданные на одном и том же множестве 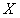 , называется функциональным рядом с общим членом
, называется функциональным рядом с общим членом 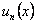 .
.
Если в функциональном ряду
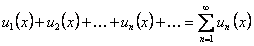 (12.2.2)
(12.2.2)
переменную x заменить любым числом x0 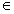 X, то получим числовой ряд
X, то получим числовой ряд
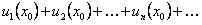
Таким образом, каждый функциональный ряд определяет множество числовых рядов, получаемых из него подстановкой вместо переменной ее значений. В зависимости от значения, принимаемого переменной 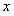 , числовой ряд (12.30) может сходиться или расходиться.
, числовой ряд (12.30) может сходиться или расходиться.
ОПРЕДЕЛЕНИЕ 12.2.6 Функциональный ряд (12.2.2) называется сходящимся в точке 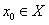 , если сходится числовой ряд
, если сходится числовой ряд 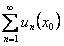 .
.
Подобно числовым рядам в функциональных рядах вводится понятие частичной суммы.
ОПРЕДЕЛЕНИЕ 12.2.7 Частичными суммами ряда 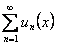 называются функции
называются функции
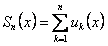 . (12.2.3)
. (12.2.3)
Итак, если 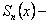 частичные суммы ряда (12.2.3), то определение 6 можно сформулировать следующим образом.
частичные суммы ряда (12.2.3), то определение 6 можно сформулировать следующим образом.
ОПРЕДЕЛЕНИЕ 12.2.8 Функциональный ряд (12.2.3) называется сходящимся в точке 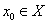 , если в этой точке сходится последовательность его частичных сумм.
, если в этой точке сходится последовательность его частичных сумм.
ОПРЕДЕЛЕНИЕ 12.2.9 Множество значений переменной 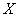 , при которых функциональный ряд
, при которых функциональный ряд 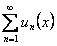 сходится, называется областью сходимости этого ряда.
сходится, называется областью сходимости этого ряда.
ОПРЕДЕЛЕНИЕ 12.2.10 Предел частичных сумм сходящегося на множестве 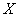 ряда (12.2.2) называется его суммой
ряда (12.2.2) называется его суммой 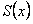 .
.
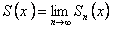 .(12.2.4)
.(12.2.4)
ПРИМЕР 12.2.10 Функциональный ряд 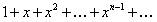 при каждом
при каждом 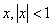 представляет убывающую геометрическую прогрессию. Значит, если
представляет убывающую геометрическую прогрессию. Значит, если 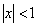 , ряд сходится. Если
, ряд сходится. Если 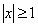 , то ряд расходится. Таким образом, область сходимости данного ряда состоит из всех тех значений переменной
, то ряд расходится. Таким образом, область сходимости данного ряда состоит из всех тех значений переменной 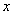 , для которых
, для которых 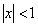 .
.
Для определения области сходимости функционального ряда можно применять известные достаточные признаки сходимости числовых рядов.
ПРИМЕР 12.1.11 Определить область сходимости функционального ряда
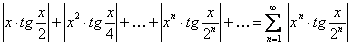 .
.
Для установления области сходимости применим признак Даламбера
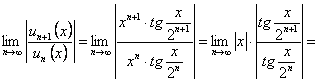
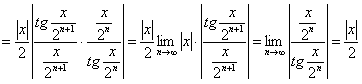 ,
,
так как 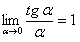 .
.
Область сходимости ряда 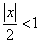 или
или 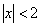 , а для всех
, а для всех 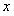 ,
, 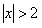 ряд расходится. Остается исследовать сходимость на границе области при
ряд расходится. Остается исследовать сходимость на границе области при 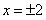 . Для этого в функциональный ряд вместо
. Для этого в функциональный ряд вместо 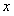 подставим
подставим 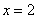 и
и 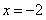 ; в результате получим числовой ряд при
; в результате получим числовой ряд при 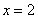
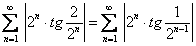 .
.
Применим необходимый признак сходимости ряда 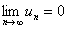 ; тогда
; тогда 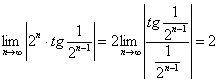 . Необходимый признак не выполняется, значит при
. Необходимый признак не выполняется, значит при 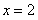 ряд расходится.
ряд расходится.
При 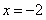 получаем ряд
получаем ряд 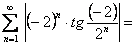
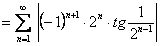 , для которого
, для которого 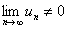 . Тогда областью сходимости функционального ряда является интервал
. Тогда областью сходимости функционального ряда является интервал 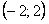 .
.
ОПРЕДЕЛЕНИЕ 12.2.11 Ряд 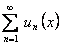 , сходящийся для всех
, сходящийся для всех 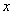 из области
из области 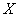 , называется равномерно сходящимся в этой области, если для каждого числа
, называется равномерно сходящимся в этой области, если для каждого числа 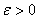 существует такой не зависящий от
существует такой не зависящий от 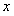 , номер
, номер 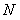 , что при
, что при 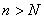 неравенство
неравенство 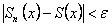 выполняется одновременно для всех
выполняется одновременно для всех 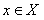 .
.
ТЕОРЕМА 12.2.5 (Признак Вейерштрасса).
Пусть даны два ряда: функциональный 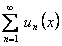 , членами которого являются функции
, членами которого являются функции 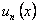 , определенные на множестве
, определенные на множестве 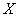 , и числовой ряд
, и числовой ряд 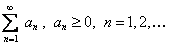 . Если числовой ряд сходится и для
. Если числовой ряд сходится и для 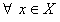 выполняется неравенство
выполняется неравенство 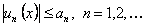 , то функциональный ряд абсолютно и равномерно сходится на множестве
, то функциональный ряд абсолютно и равномерно сходится на множестве 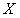 .
.
ПРИМЕР 12.2.12 Доказать, что функциональный ряд 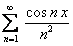 сходится равномерно на всей числовой оси.
сходится равномерно на всей числовой оси.
Решение.
Для всех 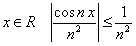 , а числовой ряд с
, а числовой ряд с 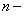 м членом
м членом 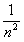 , то есть
, то есть 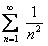 сходится. Значит ряд
сходится. Значит ряд 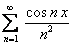 по теореме Вейерштрасса равномерно сходится на всей числовой оси.
по теореме Вейерштрасса равномерно сходится на всей числовой оси.
ТЕОРЕМА 12.2.6 Почленное интегрирование функциональных рядов.
Если функции 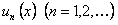 непрерывны на отрезке
непрерывны на отрезке 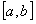 и составленный из них ряд
и составленный из них ряд 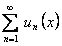 сходится равномерно на этом отрезке, и имеет суммой функцию
сходится равномерно на этом отрезке, и имеет суммой функцию 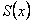 , то ряд составленный из интегралов от его членов на отрезке
, то ряд составленный из интегралов от его членов на отрезке 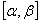 , также сходится и имеет суммой функцию
, также сходится и имеет суммой функцию 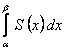 , где
, где 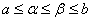 .
.
ПРИМЕР 12.2.13 Функциональный ряд 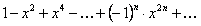 сходится равномерно при
сходится равномерно при 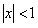 , так как при
, так как при 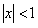 ряд является геометрической прогрессией со знаменателем меньше
ряд является геометрической прогрессией со знаменателем меньше 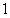 , сумма его равна
, сумма его равна 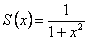 .
.
Проинтегрируем данный ряд от 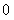 до
до 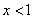 , в результате чего получим ряд
, в результате чего получим ряд
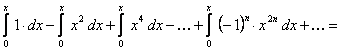
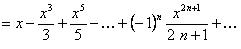 .
.
Полученный ряд сходится равномерно при 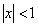 , согласно признаку Вейерштрасса. Тогда сумма полученного ряда
, согласно признаку Вейерштрасса. Тогда сумма полученного ряда 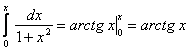 .
.
ТЕОРЕМА 12.2.7 Почленное дифференцирование функциональных рядов Пусть ряд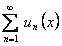 сходится на отрезке
сходится на отрезке 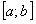 и имеет сумму
и имеет сумму 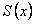 , а его члены имеют на этом отрезке непрерывные производные, причем ряд, составленный из этих производных
, а его члены имеют на этом отрезке непрерывные производные, причем ряд, составленный из этих производных 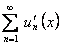 , сходится равномерно на
, сходится равномерно на 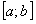 и имеет сумму
и имеет сумму 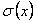 . Тогда функциональный ряд
. Тогда функциональный ряд 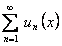 сходится на отрезке
сходится на отрезке 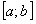 равномерно и производная его суммы равна сумме ряда
равномерно и производная его суммы равна сумме ряда 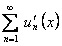 , то есть
, то есть 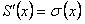 .
.
ПРИМЕР 12.2.14 Дан сходящийся на всей числовой оси функциональный ряд 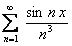 , сумма которого
, сумма которого 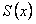 . Ряд, составленный из производных, то есть полученный из данного дифференцированием его членов
. Ряд, составленный из производных, то есть полученный из данного дифференцированием его членов 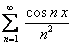 , равномерно сходится на всей числовой оси, согласно признаку Вейерштрасса.
, равномерно сходится на всей числовой оси, согласно признаку Вейерштрасса.
Покажем, что 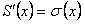 , где
, где 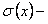 сумма ряда
сумма ряда 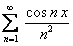 . Данный
. Данный
ряд 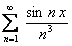 и ряд
и ряд 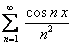 удовлетворяют условиям теоремы 12.10
удовлетворяют условиям теоремы 12.10
Следовательно, по доказанной теореме 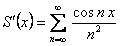 , то есть
, то есть 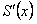 равна
равна 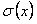 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >