Пусть дана система двух дискретных случайных величин 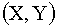 , возможные значения СВ
, возможные значения СВ 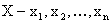 , СВ
, СВ 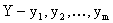 , соответствующее вероятности
, соответствующее вероятности 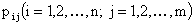 .
.
Тогда математические ожидания и дисперсии составляющих случайных величин
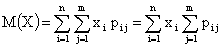 ,
,
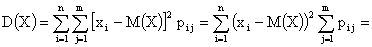 ,
,
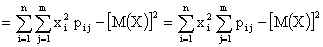 ,
,
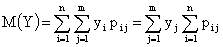 ,
,
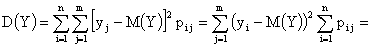 ,
,
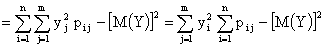 .
.
Если система двух непрерывных случайных величин задана плотностью вероятностей 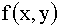 , то
, то
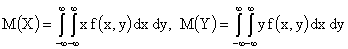 ,
,
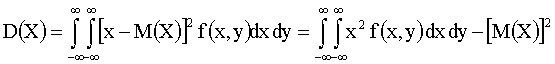 ,
,
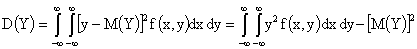 .
.
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент (ковариация) и коэффициент корреляции.
Корреляционным моментом 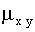 случайных величин X и Y называют математическое ожидание произведения отклонений этих величин
случайных величин X и Y называют математическое ожидание произведения отклонений этих величин
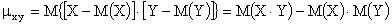 ,
,
Для вычисления корреляционного момента дискретных величин используют формулу
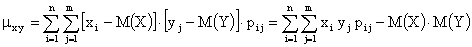 ,
,
для непрерывных величин – формулу
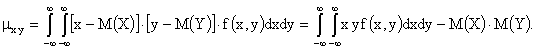 .
.
Коэффициентом корреляции 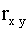 величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
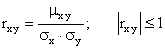 .
.
Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.
Для независимых случайных величин выполняются следующие свойства:
1. 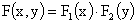 ,
,
2. 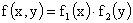 .
.
Корреляционный момент 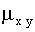 и коэффициент корреляции
и коэффициент корреляции 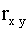 служат для характеристики связи между величинами X и Y.
служат для характеристики связи между величинами X и Y.
Если X и Y независимы, то корреляционный момент равен нулю. Обратное не всегда верно: если 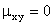 , то не всегда X и Y независимые случайные величины.
, то не всегда X и Y независимые случайные величины.
Коэффициент корреляции служит для оценки тесноты линейной связи между X и Y. Если между случайными величинами существует строгая функциональная линейная зависимость: 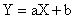 , то
, то 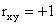 при
при 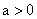 и
и 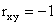 при
при 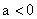 , причем, чем ближе абсолютная величина
, причем, чем ближе абсолютная величина 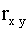 к единице, тем линейная связь сильнее. Если
к единице, тем линейная связь сильнее. Если 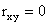 , это означает только отсутствие линейной связи между случайными величинами; любой другой вид связи может при этом присутствовать.
, это означает только отсутствие линейной связи между случайными величинами; любой другой вид связи может при этом присутствовать.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 13.2.53. Матрица распределения системы двух дискретных случайных величин 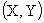 задана таблицей
задана таблицей
| X\Y | 0 | 2 | 5 |
| 1 | 0,1 | 0,1 | 0,2 |
| 2 | 0,2 | 0,3 | 0,1 |
Найти числовые характеристики системы 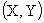 .
.
Решение.
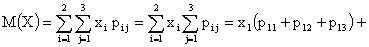
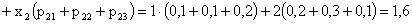
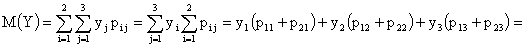

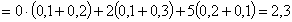
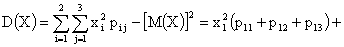
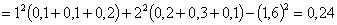
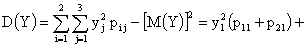
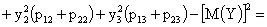
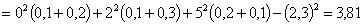
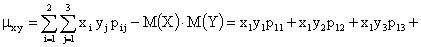
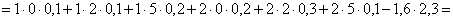
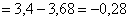
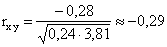
ПРИМЕР 13.2.54. Пусть область D возможных значений двумерной случайной величины – треугольник с границами 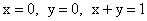 .Плотность распределения имеет вид
.Плотность распределения имеет вид 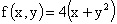 . Найдем числовые характеристики системы.
. Найдем числовые характеристики системы.
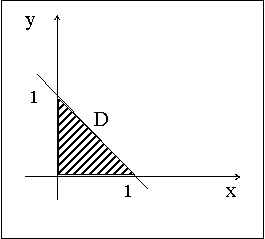
Решение.
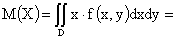
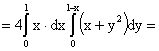
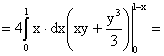
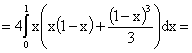
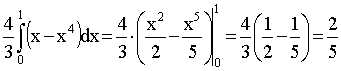
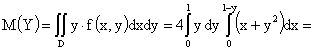
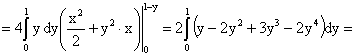
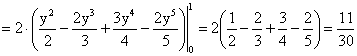
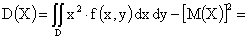
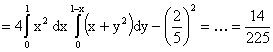
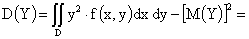
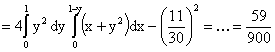
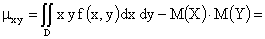
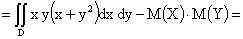
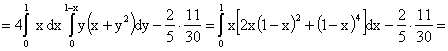
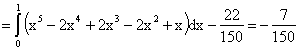
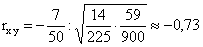 ,
,
что показывает, что между случайными величинами X и Y существует отрицательная линейная зависимость, то есть при увеличении одной из них другая имеет некоторую тенденцию уменьшаться.
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулы расчета числовых характеристик системы двух случайных величин
3.2.12.1. Закон распределения двумерной случайной величины:
| X\Y | 0 | 2 |
| 0 | 0,15 | 0,25 |
| 1 | 0,2 | 0,15 |
| 2 | 0,05 | 0,20 |
а) Определить закон распределения случайной компоненты X. Найти M(X) и D(X).
б) Проделать то же самое для случайной компоненты Y.
в) Найти коэффициент корреляции.
Отв.:
| X | 0 | 1 | 2 |
| P | 0,4 | 0,35 | 0,25 |
| Y | 0 | 2 |
| P | 0,4 | 0,6 |
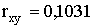
3.2.12.2. Бросаются две неразличимые игральные кости. Пусть X — сумма выпавших очков, а Y — разность между большим и меньшим числом очков на костях.
а) Построить двумерный ряд распределения.
б) Определить математическое ожидание и дисперсию компонент.
в) Найти коэффициент корреляции системы (X,Y).
Отв.:
| X\Y | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 |
| 1 | 0 | 2/36 | 0 | 2/36 | 0 | 2/36 | 0 | 2/36 | 0 | 2/36 | 0 |
| 2 | 0 | 0 | 2/36 | 0 | 2/36 | 0 | 2/36 | 0 | 2/36 | 0 | 0 |
| 3 | 0 | 0 | 0 | 2/36 | 0 | 2/36 | 0 | 2/36 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 2/36 | 0 | 2/36 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 2/36 | 0 | 0 | 0 | 0 | 0 |
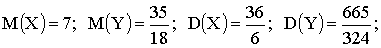
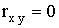
3.2.12.3. Решить предыдущую задачу в предположении, что кости помеченные, а СВ Y — разность очков на костях.
Отв.:
| X\Y | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| -5 | 0 | 0 | 0 | 0 | 0 | 1/36 | 0 | 0 | 0 | 0 | 0 |
| -4 | 0 | 0 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 0 | 0 | 0 |
| -3 | 0 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 0 | 0 |
| -2 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 0 |
| -1 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 |
| 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 |
| 1 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 |
| 2 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1/36 | 0 | 0 | 0 | 0 | 0 |
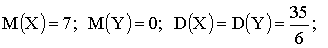
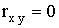
3.2.12.4. Непрерывная двумерная случайная величина (X,Y) распределена равномерно внутри прямоугольника с центром симметрии в начале координат и сторонами 2a и 2b, параллельными координатным осям.
Найти: а) двумерную плотность вероятности системы; б) плотности распределения составляющих; в) показать, что СВ X и Y независимы и 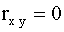 .
.
Отв.: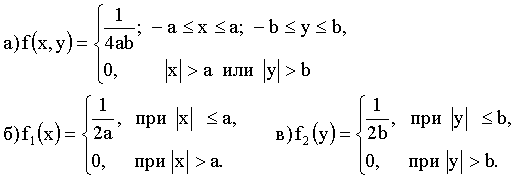
3.2.12.5. Двумерная случайная величина (X,Y) задана плотностью распределения 
а) Найти плотности распределения составляющих и показать, что X и Y зависимые.
б) Найти корреляционный момент 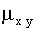 .
.
Указание. Воспользоваться свойством определенного интеграла: если подынтегральная функция нечетна и пределы интегрирования симметричны относительно начала координат, то определенный интеграл равен нулю.
Отв.:
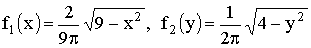 внутри эллипса
внутри эллипса
и 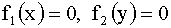 вне его
вне его
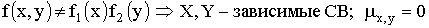
3.2.12.6. Задана плотность совместного распределения непрерывной двумерной случайной величины (X,Y): 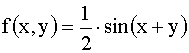 в квадрате
в квадрате 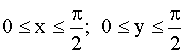 ; вне квадрата
; вне квадрата 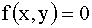 . Найти математические ожидания и дисперсии составляющих.
. Найти математические ожидания и дисперсии составляющих.
Отв.: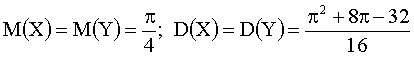
3.2.12.7. Плотность распределения двумерной непрерывной случайной величины 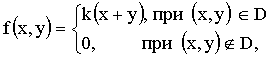
где D — треугольная область плоскости, координаты точек которых положительны, но лежат ниже прямой 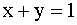 . Определить:
. Определить:
а) нормировочный множитель k;
б) математические ожидания и дисперсии составляющих X и Y;
в) коэффициент корреляции между X и Y;
г) вероятность события 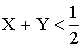 ;
;
д) плотность распределения СВ X.
Отв.:
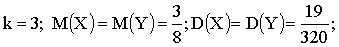
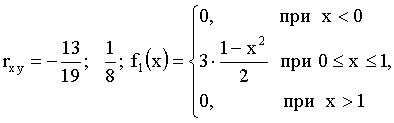
3.2.12.8. Плотность распределения двумерной непрерывной случайной величины 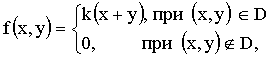
где 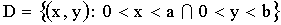 .
.
Определить:
а) нормировочный множитель k;
б) математические ожидания и дисперсии X и Y;
в) коэффициент корреляции между X и Y;
г) вероятность 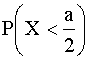 ;
;
д) функцию распределения случайной величины Y.
Отв.:
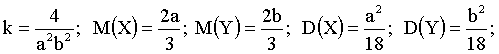
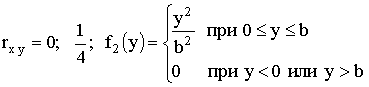
3.2.12.9. Независимые случайные величины 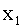 и
и 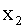 имеют математические ожидания
имеют математические ожидания 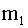 и
и 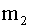 и дисперсии
и дисперсии 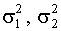 соответственно. Рассмотрим новые случайные величины
соответственно. Рассмотрим новые случайные величины 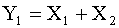 и
и 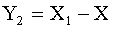 . Найти коэффициент корреляции между случайными величинами
. Найти коэффициент корреляции между случайными величинами 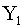 и
и 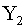 .
.
Отв.:
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >