Интегрирование и дифференцирование степенных рядов

ТЕОРЕМА 12.1.15 Степенной ряд 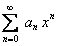в промежутк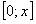е , где 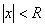, всегда можно интегрировать почленно, то есть

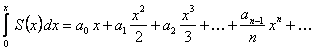где 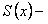сумма ряда.

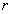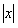Доказательство. Выберем число между и 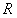. Тогда ряд 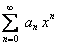сходится равномерно на отрезке 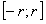, а по теореме о почленном интегрировании функциональных рядов на отрезке 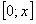ряд можно почленно интегрировать.

ТЕОРЕМА 12.1.16 Степенной ряд 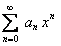внутри его интервала сходимости можно дифференцировать почленно, то есть

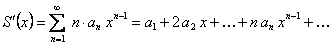где 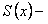сумма ряда.

Онлайн помощь

Доказательство. Для любого 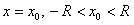можно выбрать два числа 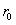и 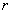так, чтобы 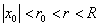. Ввиду сходимости ряда 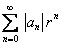его общий член ограничен: .

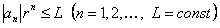Тогда при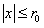

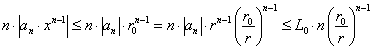где .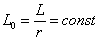

Члены ряда 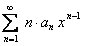для указанных значений 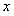, не превосходят соответствующих членов ряда:

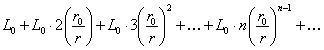. (12.1.45)

Принимая во внимание, что 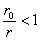, ряд (1) по признаку Даламбера сходится. Поэтому ряд 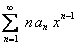на отрезке 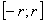сходится равномерно, а по теореме о почленном дифференцировании функциональных рядов ряд 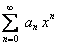можно почленно дифференцировать на отрезке 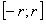и, в частности, при .

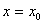Следствие 1. Степенной ряд 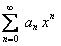в интервале сходимости можно почленно дифференцировать любое число раз, причем ряды, полученные в результате дифференцирования, сходятся в том же интервале.

Замечание. В теоремах (12.1.14) и (12.1.15) показано, что ряды 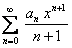и 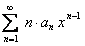сходятся на интервале 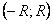, следовательно, их радиусы сходимости не меньше 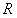. Но, в свою очередь, ряд 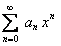получается почленным дифференцированием ряда 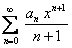и почленным интегрированием ряда 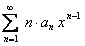, так что 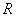не может быть меньше упомянутых радиусов 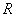. Из сказанного вытекает, что радиусы сходимости рядов 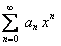, 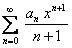и 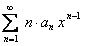равны между собой.