Дан ряд 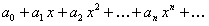 . Рассмотрим ряд, составленный из абсолютных величин его членов:
. Рассмотрим ряд, составленный из абсолютных величин его членов:
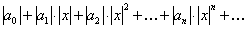 .(12.1.42)
.(12.1.42)
Для определения сходимости ряда (12.42) применим признак Даламбера, то есть определим 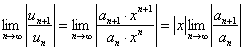 ;
;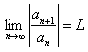 , тогда
, тогда 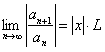 . Тогда по признаку Даламбера ряд (12.42) сходится, если
. Тогда по признаку Даламбера ряд (12.42) сходится, если 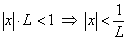 (
(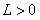 , так как ряд (12.1.42) с положительными членами), и расходится, если
, так как ряд (12.1.42) с положительными членами), и расходится, если 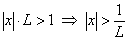 .
.
Итак, из сходимости ряда (12.1.42) при 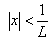 следует абсолютная сходимость ряда
следует абсолютная сходимость ряда 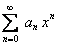 . Из вышеизложенного интервал сходимости ряда
. Из вышеизложенного интервал сходимости ряда 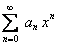 будет иметь вид
будет иметь вид 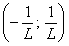 . Значит,
. Значит,
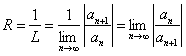 (12.1.43)
(12.1.43)
Аналогично для определения радиуса сходимости можно использовать признак Коши
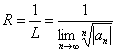 .(12.1.44)
.(12.1.44)
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >