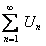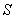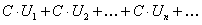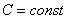ТЕОРЕМА 12.1.2 Если ряд сходится и его сумма равна , то ряд , где , также сходится и его сумма равна .

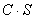Доказательство. Обозначим 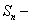частичную сумму ряда

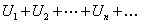и 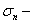частичную сумму ряда

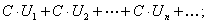тогда

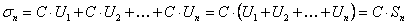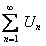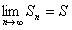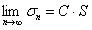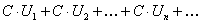, а так как ряд сходится, то . Следовательно, , ряд сходится и его сумма равна .

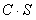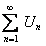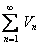ТЕОРЕМА 12.1.3 Если ряды и сходятся и их суммы соответственно равны 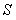и 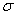, то и ряд 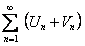сходится и его сумма равна :

.

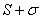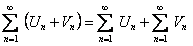Доказательство. Пусть

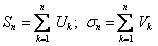и ,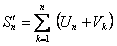

тогда .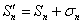

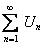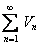По условию ряды и сходятся, а это значит, что

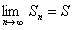и 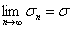и предел 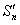существует при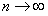

, что

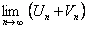сходится и его сумма равна 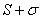. Таким образом, сумма двух сходящихся рядов является сходящимся рядом.

Замечание. Разность двух сходящихся рядов 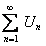и 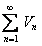есть ряд сходящийся, так как ряд 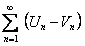является суммой двух сходящихся рядов 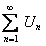и .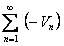

ТЕОРЕМА 12.1.4 Сходимость ряда не изменится, если отбросить или добавить конечное число членов (без доказательства).

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >