Мы называли две величины независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых величин равны их безусловным распределениям.

Выведем необходимые и достаточные условия независимости случайных величин.

ТЕОРЕМА 13.1.17. Для того, чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения системы (X,Y) была равна произведению функций распределения составляющих:

.

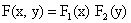Доказательство. а) Необходимость. Пусть X и Y независимы. Тогда события X < x и Y < y независимы, следовательно, вероятность совмещения этих событий равна произведению их вероятностей:

P(X < x, Y < y) = P(X < x) P(Y < y),

или

.

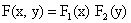б) Достаточность. Пусть 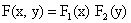. Отсюда

P(X < x, Y < y) = P(X < x) P(Y < y),

т. е. вероятность совмещения событий X < x и Y < y равна произведению вероятностей этих событий. Следовательно, случайные величины X и Y независимы.

Следствие. Для того, чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих:

.

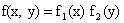Доказательство.

а) Необходимость. Пусть X и Y – независимые непрерывные случайные величины. Тогда (на основании предыдущей теоремы) .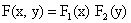

Дифференцируя это равенство по x, затем по y, имеем

или (по определению плотностей распределения двумерной и одномерной величин)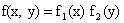

б) Достаточность. Пусть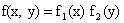

Интегрируя это равенство по x и по y, получим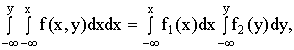

или .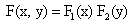

Отсюда (на основании предыдущей теоремы) заключаем, что X и Y независимы.

Замечание. Так как приведенные выше условия являются необходимыми и достаточными, можно дать новые определения независимых случайных величин:

1) две случайных величины называют независимыми , если функция распределения системы этих величин равна произведению функций распределения составляющих;

2) две непрерывные случайные величины называют независимыми , если плотность совместного распределения системы этих величин равна произведению плотностей распределения составляющих.

ПРИМЕР 13.1.59 Двумерная непрерывная случайная величина (X,Y) задана плотностью совместного распределения
f(x,y) = (sin(x) sin(y)) / 4 в квадрате 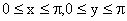; вне этого квадрата f(x,y)=0.

Доказать, что составляющие X и Y независимы.

Решение. Используя предыдущие формулы, легко найдем плотности распределения составляющих: 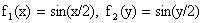. Плотность совместного распределения рассматриваемой системы равна произведению плотностей распределения составляющих, поэтому X и Y независимы.

Разумеется, можно было доказать, что условные законы распределения составляющих равны их безусловным законам, откуда также следует независимость X и Y.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >