Рассмотрим двумерную случайную величину (X,Y), где X и Y — зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X:

,

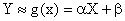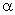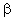где и — параметры, подлежащие определению. Это можно сделать различными способами, наиболее обоснованный из которых – метод наименьших квадратов.

Функцию 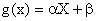называют “наилучшим приближением” Y в смысле метода наименьших квадратов, если математическое ожидание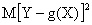
принимает наименьшее возможное значение; функцию g(x) называют среднеквадратической регрессией Y на X .

Помощь по математике

ТЕОРЕМА 13.1.21. Линейная средняя квадратическая регрессия Y на X имеет вид

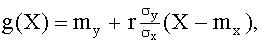
где ,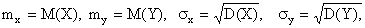

где 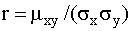— коэффициент корреляции величин X и Y.

Доказательство. Введем в рассмотрение функцию двух независимых аргументов 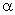и :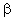

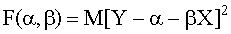. (13.1.54)

Учитывая, что

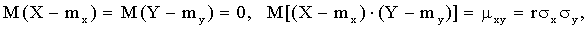и выполнив выкладки, получим

.

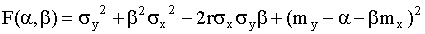Исследуем функцию 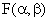на экстремум, для чего приравняем нулю частные производные:

.

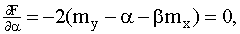
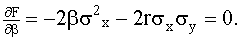Отсюда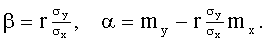

Легко убедиться, что при этих значениях 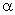и 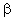рассматриваемая функция принимает наименьшее значение.

Итак, линейная средняя квадратическая регрессия Y и X имеет вид

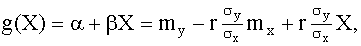
или

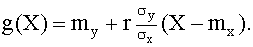
Коэффициент 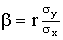называют коэффициентом регрессии Y на X , а прямую

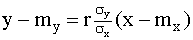(13.1.55)

называют прямой среднеквадратической регрессии Y на X.

Подставив найденные значения 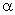и 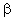в соотношение (13.1.54), получим минимальное значение функции 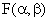, равное .

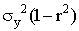Величину 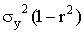называют остаточной дисперсией случайной величины Y относительно случайной величины X; она характеризует величину ошибки, которую допускают при замене Y линейной функцией .

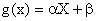При 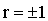остаточная дисперсия равна нулю; другими словами, при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении Y в виде линейной функции от X.

Итак, если коэффициент корреляции 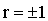, то Y и X связаны линейной функциональной зависимостью.

Аналогично можно получить прямую среднеквадратической регрессии X на Y:

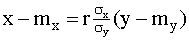(13.1.56)

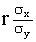— коэффициент регрессии X на Y и остаточную дисперсию 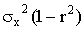величины X относительно Y.

Если 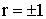, то обе прямые регрессии, как видно из (13.1.55) и (13.1.56), совпадают.

Из уравнений (13.1.55) и (13.1.56) следует, что обе прямые регрессии проходят через точку 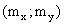, которую называют центром совместного распределения величин X и Y.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >