Вероятностью Р(А) случайного события А называется число, около которого группируются относительные частоты этого события при неограниченном увеличении числа испытаний. Символически это можно записать так:
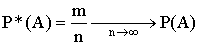
Рассмотрим свойства относительной частоты, вытекающие из её определения:
- Относительная частота случайного события А есть неотрицательное число, удовлетворяющее неравенству
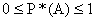 .
.
Из этого следует, что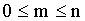 ,
, 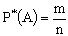
- Относительная частота достоверного события
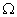 равна единице:
равна единице: 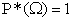 , т.к. m=n для события
, т.к. m=n для события 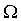 .
. - относительная частота невозможного события
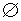 равна нулю:
равна нулю: 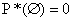 , т.к. m=0 для события
, т.к. m=0 для события 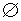
- Относительная частота суммы двух несовместных событий A и B равна сумме относительных частот событий (правило сложения относительных частот): P*(A+B)=P*(A)+P*(B).
- Правило умножения относительных частот для совместных событий: относительная частота произведения двух совместных событий равна произведению относительной частоты одного из них на условную относительную частоту другого:
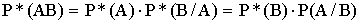
Доказательство: 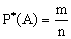 ,
, 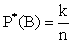
, где m – частота наступления события А, k – частота наступления события В. Тогда частота наступления события А+В будет равна m+k, т.к. они несовместны. Имеем 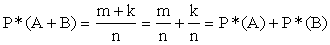
Для совместных событий А и В введены понятия условной относительной частоты. Условной относительной частотой называется относительная частота одного события, вычисленная при условии наступления другого события. Обозначения условной относительной частоты: P*(A/B), P*(B/A).
Доказательство: Пусть в серии из n опытов событие А наступило m раз, В – k раз, АВ – l раз. Тогда
 ,
,
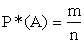 ,
,
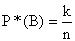 ,
,
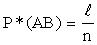 ,
,
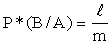 ,
,
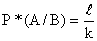 .
.
Имеем 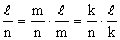
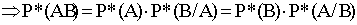 .
.
В силу определения этими же свойствами должны обладать статистические вероятности событий.
Статистическое определение вероятности отражает суть понятия вероятности как меры объективной возможности наступления события. Зная вероятность события, можно, не производя испытаний, предсказать, насколько часто оно будет наступать при большом числе испытаний. Если вероятность событий мала, то оно будет редко появляться при большом числе испытаний, и практически можно считать, что при единичном испытании это событие не наступит (принцип практической невозможности маловероятных событий). Если случайное событие имеет вероятность, близкую к единице, то практически можно считать, что в единичном испытании это событие наступит. Здесь речь идёт о практической, а не об абсолютной уверенности, так как абсолютно точно предсказать результат испытания со случайным исходами нельзя. Данное испытание может оказаться тем редким испытанием, в котором появится событие, имеющее вероятность, близкую к нулю, а событие, имеющее вероятность, близкую к единице, не наступит. Вопрос о том, какую вероятность считать близкой к нулю или единице, зависит от существа задачи.
Достоинством статистического определения вероятности является его опора на испытания (практику). Для существования статистической вероятности требуется:
- Возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие A может наступить или не наступить.
- Устойчивость относительных частот (чаcтостей) появления события А для разных серий при достаточно большом числе испытаний.
Недостатки статистического определения вероятности:
- для нахождения вероятности требуются материальные затраты на испытания;
- по результатам испытаний находится лишь приближенная оценка неизвестной вероятности, а не ее точное значение;
- оно не позволяет непосредственно вычислять вероятность (по определению).
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >