Свойство 1. Плотность распределения — неотрицательная функция: .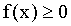

Доказательство. Функция распределения — неубывающая функция, следовательно, ее производная 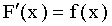— функция неотрицательная.

С геометрической точки зрения это означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью Ох, либо на этой оси.

График плотности распределения называют кривой распределения .

Свойство 2. Несобственный интеграл от плотности распределения в пределах от 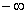до 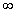равен единице:

.

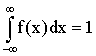Доказательство. Несобственный интеграл 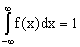выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу 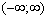. Очевидно, такое событие достоверно, следовательно, вероятность его равна единице.

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.

В частности, если все возможные значения случайной величины принадлежат интервалу (a;b), то

.

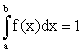ПРИМЕР 13.1.44 Плотность распределения случайной величины Х задана:

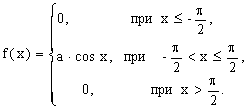
Найти постоянный параметр а.

Решение

.

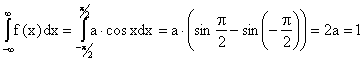Таким образом, искомый параметр .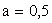

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >