Свойство 1. Значения функции распределения принадлежат отрезку [0;1]:
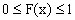 .
.
Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.
Свойство 2. F (х) — неубывающая функция, т. е.
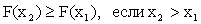 .
.
Доказательство. Пусть 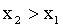 . Событие, состоящее в том, что Х примет значение, меньшее
. Событие, состоящее в том, что Х примет значение, меньшее 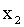 , можно подразделить на следующие два несовместных события:
, можно подразделить на следующие два несовместных события:
1) Х примет значение, меньшее 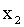 , с вероятностью
, с вероятностью 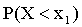 ;
;
2) Х примет значение, удовлетворяющее неравенству 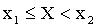 , с вероятностью
, с вероятностью 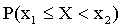 . По теореме сложения имеем
. По теореме сложения имеем 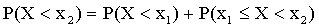 .
.
Отсюда
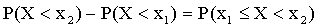
или
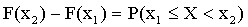 .
.
Так как любая вероятность есть число неотрицательное, то
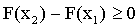
или
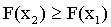 .
.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a;b), равна приращению функции распределения на этом интервале:
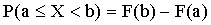 .
.
Это важное следствие вытекает из свойства 2, если
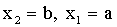 .
.
ПРИМЕР 13.1.40 Случайная величина Х задана функцией распределения: 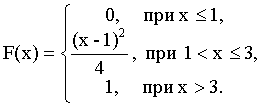
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (1;2).
Решение. Так как на интервале (1;2), по условию,
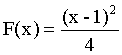 ,
,
то
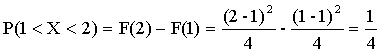 .
.
Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
Действительно, положив
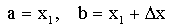
в формуле 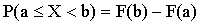 ,
,
имеем
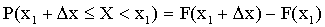 .
.
Пусть 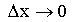 . Тогда в силу непрерывности функции F(х) (Х — непрерывная случайная величина)
. Тогда в силу непрерывности функции F(х) (Х — непрерывная случайная величина) 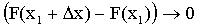 ;
;
следовательно, 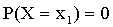 .
.
Тогда 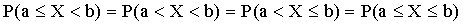 .
.
Например, равенство 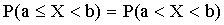 доказывается так:
доказывается так:
 .
.
Замечание. Ранее мы уже встречались с событиями, вероятности которых были равны нулю, – невозможные события. Теперь же рассматриваются события возможные, но с нулевой вероятностью. Они появляются только при рассмотрении опытов, не сводящихся к схеме случаев. Понятие о событии “возможном, но обладающем нулевой вероятностью”, не более парадоксально, чем представление о фигуре, имеющей определенную площадь, тогда как ни одна из точек внутри фигуры отличной от нуля площадью не обладает. Фигура состоит из таких точек, но ее площадь не равна сумме их площадей. Сколь угодно малый элемент, выделенный из этой фигуры, имеет площадь; она приближается к нулю при уменьшении размеров элемента и в пределе равна нулю для точки.
Если производится опыт, в котором непрерывная случайная величина должна принять одно из своих возможных значений, то до опыта вероятность каждого из таких значений равна нулю. Однако в исходе опыта случайная величина непременно примет одно из своих возможных значений, т.е. заведомо произойдет одно из событий, вероятности которых были равны нулю.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а;b), то:
1) 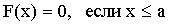 ;
;
2) 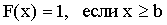 .
.
Доказательство. 1) Пусть  . Тогда событие
. Тогда событие 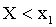 невозможно (так как значений, меньших
невозможно (так как значений, меньших 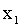 , величина Х по условию не принимает) и,следовательно, вероятность его равна нулю.
, величина Х по условию не принимает) и,следовательно, вероятность его равна нулю.
2) Пусть 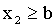 . Тогда событие
. Тогда событие  достоверно (так как все возможные значения Х меньше
достоверно (так как все возможные значения Х меньше 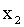 ) и, следовательно, вероятность его равна единице.
) и, следовательно, вероятность его равна единице.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:
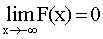 ,
, 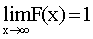 .
.
Сформулированные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми 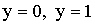 (первое свойство).
(первое свойство).
При возрастании х в интервале (a;b), в котором заключены все возможные значения случайной величины, ордината точек графика возрастает (второе свойство).
При 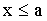 ординаты графика равны нулю; при
ординаты графика равны нулю; при 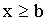 ординаты графика равны единице (третье свойство).
ординаты графика равны единице (третье свойство).
График функции распределения непрерывной случайной величины изображен на рис.13.1.3.
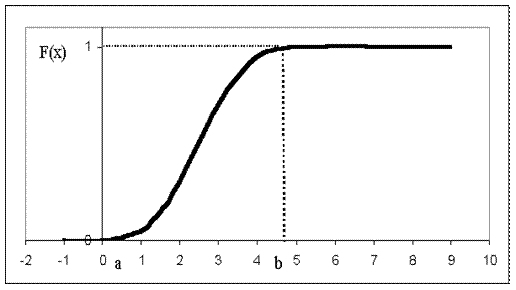
Функция распределения дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. Сумма всех скачков функции F(X) равна единице.
ПРИМЕР 13.1.41 Дискретная случайная величина Х задана таблицей распределения
| X | -1 | 2 | 5 |
| p | 0,2 | 0,3 | 0,5 |
Найти функцию распределения и построить ее график.
Решение. Если 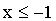 , то
, то 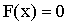 (третье свойство).
(третье свойство).
Если  , то
, то 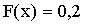 , т.к. Х может принять единственное возможное в данном случае значение -1 с вероятностью 0,2.
, т.к. Х может принять единственное возможное в данном случае значение -1 с вероятностью 0,2.
Если  , то
, то 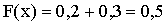 . Действительно, т.к. Х может принять значение -1 (вероятность этого события равна 0,2) или значение 2
. Действительно, т.к. Х может принять значение -1 (вероятность этого события равна 0,2) или значение 2
(вероятность этого события равна 0,3). Поскольку эти два события несовместны, то по теореме сложения вероятность события Х < х равна сумме вероятностей 0,2+0,3=0,5.
Если 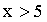 , то
, то 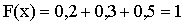 . Действительно, событие
. Действительно, событие 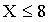 достоверно, следовательно, его вероятность равна единице.
достоверно, следовательно, его вероятность равна единице.
Итак, функция распределения аналитически может быть записана так:
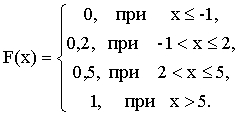
График этой функции приведен на рис.13.1.4.
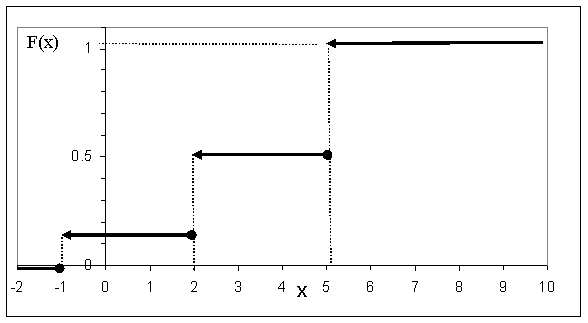
По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки – меньше; ступенчатая кривая становится более плавной (рис.13.1.5.).
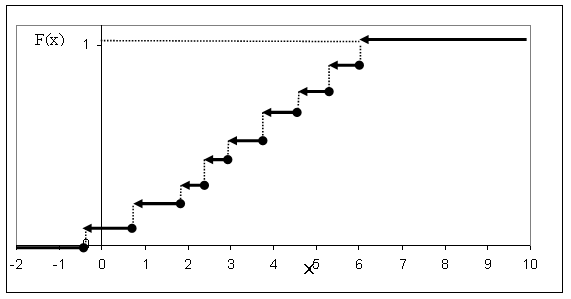
Cлучайная величина постепенно приближается к непрерывной величине, а ее функция распределения – к непрерывной функции (рис.13.1.3.).
На практике обычно функция распределения непрерывной случайной величины представляет собой функцию, непрерывную во всех точках. Однако можно построить примеры случайных величин, возможные значения которых непрерывно заполняют некоторый промежуток, но для которых функция распределения не везде является непрерывной, а в отдельных точках терпит разрывы, такие случайные величины называются смешанными.
В качестве примера смешанной случайной величины можно привести площадь разрушений, наносимых цели бомбой, радиус разрушительного действия которой равен R (рис.13.1.6).
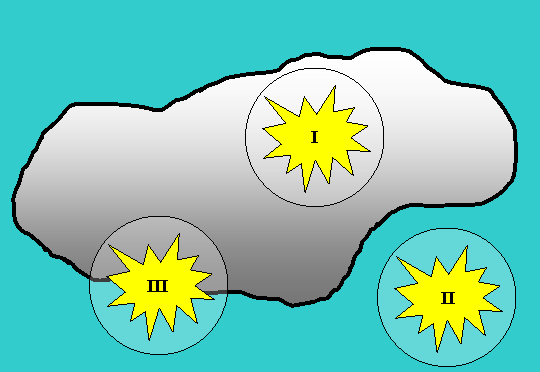
Значения этой случайной величины непрерывно заполняют промежуток 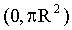 , но при этом крайние значения промежутка 0 и
, но при этом крайние значения промежутка 0 и 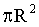 , осуществляющиеся при положении бомбы типа I и II, обладают определенной конечной вероятностью, и этим значениям соответствуют скачки функции распределения, тогда как в промежуточных значениях (положение типа III) функция распределения непрерывна (рис.13.1.7).
, осуществляющиеся при положении бомбы типа I и II, обладают определенной конечной вероятностью, и этим значениям соответствуют скачки функции распределения, тогда как в промежуточных значениях (положение типа III) функция распределения непрерывна (рис.13.1.7).
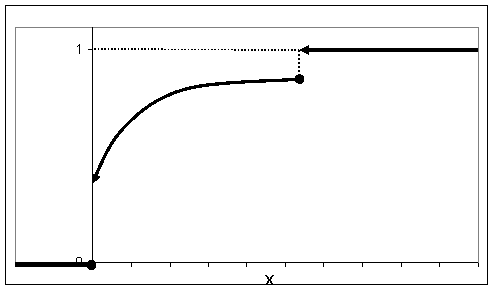
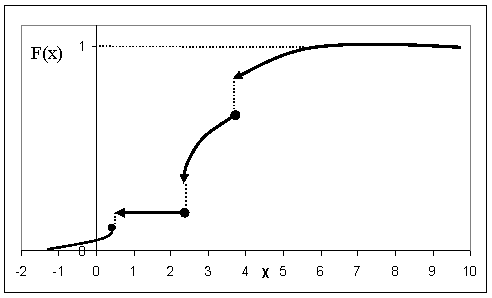
Итак, в общем случае функция распределения случайной величины может иметь график со скачками (разрывы I рода), который на отдельных участках может быть постоянной величиной, на других – монотонно возрастать (рис.13.1.8).
Онлайн помощь по математике
Лекции по высшей математике
Примеры решения задач