Пусть произведено n испытаний, в которых случайная величина Х приняла 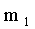раз значение 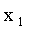, 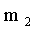раз значение 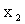, 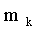раз значение 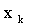, причем

.

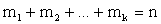Тогда сумма всех значений, принятых X, равна

.

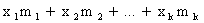Найдем среднее арифметическое 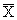всех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытаний:

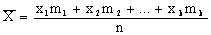
или

.

Помощь с решением

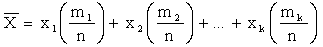Заметив, что отношение — относительная частота 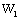значения 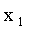, 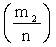— относительная частота 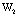значения 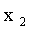и т.д.,запишем соотношение для 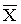так:

.

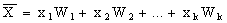Допустим, что число испытаний достаточно велико. Тогда относительная частота приближенно равна вероятности появления события:

,

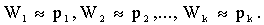Заменяя далее относительные частоты соответствующими вероятностями, получим

.

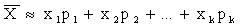Правая часть этого приближенного равенства есть М (X). Итак,

.

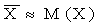Вероятностный смысл полученного результата таков: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Замечание. Очевидно, что математическое ожидание больше наименьшего и меньше наибольшего возможных значений. Таким образом, на числовой оси возможные значения расположены слева и справа от математического ожидания. С этой точки зрения математическое ожидание характеризует расположение распределения и поэтому его часто называют центром распределения.

Этот термин заимствован из механики: если массы 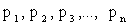расположены в точках с абсциссами .

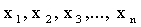Причем

,

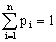то абсцисса центра тяжести

.

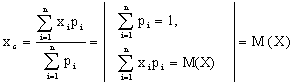Итак, математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы — их вероятностям (см. пример 13.1.29).

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >