Пусть производится n независимых испытаний, в каждом из которых может появиться, либо не появиться событие А. Пусть вероятность появления события А в каждом испытании одна и та же.
Обозначим 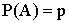 ;
; 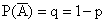 .
.
Поставим задачу вычислить вероятность того, что при испытаниях событие А наступит ровно m раз. Искомую вероятность обозначим 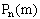 , где
, где 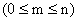 .
.
Решение. Имеем схему независимых испытаний в одинаковых условиях Бернулли: 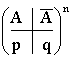 .
.
Результаты одной серии испытаний, в которой событие А наступило ровно m раз, запишем в виде таблицы, где единица соответствует наступлению события A, а ноль – наступлению 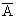 :
:
| Испытания | 1 | 2 | 3 | 4 | 5 | … | … | … | n-1 | n |
| Событие | 1 | 0 | 1 | 1 | 0 | … | … | … | 0 | 1 |
| Вероятность | p | q | p | p | q | … | … | … | q | p |
Очевидно, что сумма единиц во второй строке таблицы должна равняться m, а число нулей равно n-m . Вероятность появления данной комбинации по теореме умножения вероятностей для независимых событий равна 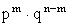 . Число же различных комбинаций наступления события А m раз в серии из n испытаний будет равно числу способов расстановки m единиц по n клеткам, что дает
. Число же различных комбинаций наступления события А m раз в серии из n испытаний будет равно числу способов расстановки m единиц по n клеткам, что дает 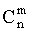 . Так как все комбинации представляют собой несовместные события, то по теореме о вероятности суммы несовместных событий получаем, что искомая вероятность будет равна
. Так как все комбинации представляют собой несовместные события, то по теореме о вероятности суммы несовместных событий получаем, что искомая вероятность будет равна
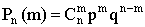 (13.1.25)
(13.1.25)
Формула (1.25) называется формулой Бернулли. Вероятности 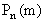
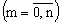 называют биномиальными, так как правая часть формулы (13.1.25) равна коэффициенту при
называют биномиальными, так как правая часть формулы (13.1.25) равна коэффициенту при 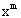 в разложении бинома
в разложении бинома 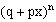 по степеням x :
по степеням x :
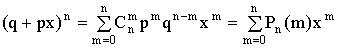 . (13.1.26)
. (13.1.26)
Функция 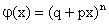 , обладающая тем свойством, что коэффициент при
, обладающая тем свойством, что коэффициент при 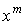 в разложении (13.1.26) дает вероятность
в разложении (13.1.26) дает вероятность 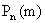 наступления события А в серии из n независимых испытаний, проводимых в одинаковых условиях, ровно m раз, называется производящей функцией для
наступления события А в серии из n независимых испытаний, проводимых в одинаковых условиях, ровно m раз, называется производящей функцией для 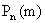 .
.
Из формулы (13.1.26) при x=1 с учетом того, что 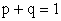 , получаем
, получаем
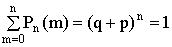 . (13.1.27)
. (13.1.27)
Этот результат (сумма всех биномиальных коэффициентов равна 1) можно было предвидеть, так как в (13.1.27) суммируются вероятности для полной группы несовместных событий.
ПРИМЕР 13.1.18 Вероятность того, что расход электроэнергии в продолжении одних суток не превысит установленной нормы, равна 0,8. Найти вероятность того, что в ближайшие 5 суток расход электроэнергии в течение 2 суток не превысит нормы.
Решение. Имеем схему Бернулли:
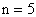 ,
, 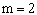 ,
, 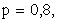 ,
, 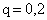 . По формуле Бернулли находим:
. По формуле Бернулли находим:
 .
.
Рассмотрим еще ряд задач, которые решаются с использованием формулы Бернулли.
Обозначим 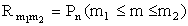 — вероятность того, что в n испытаниях схемы Бернулли событие А наступит от
— вероятность того, что в n испытаниях схемы Бернулли событие А наступит от 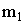 до
до 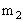 раз
раз 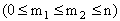 .
.
Тогда имеет место формула
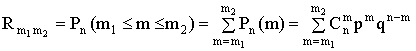 . (13.1.28)
. (13.1.28)
В частности, вероятность 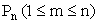 того, что в n испытаниях событие А наступит хотя бы один раз, равна
того, что в n испытаниях событие А наступит хотя бы один раз, равна
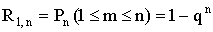 ; (13.1.29)
; (13.1.29)
вероятность того, что событие А в n испытаниях наступит не менее k раз, равна
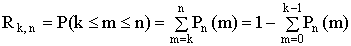 . (13.1.30)
. (13.1.30)
ПРИМЕР 13.1.19 Планируется нанесение бомбового удара по цели, для поражения которой необходимо попадание хотя бы одной бомбы. Вероятность попадания в цель одной бомбы равна 0,3. Определить необходимое количество бомб для поражения цели с гарантированной вероятностью 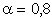 .
.
Решение. Имеем схему Бернулли, 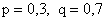 .
.
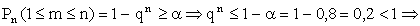 ,
,
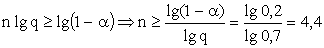 .
.
Вывод: для поражения цели с 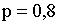 необходимо не менее 5 бомб.
необходимо не менее 5 бомб.
.
Если независимые испытания проводятся с изменением условий, то правило вычисления вероятностей 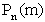 можно сформулировать так: если производится n независимых испытаний по схеме Бернулли, причем вероятность наступления события А в i — м испытании равна
можно сформулировать так: если производится n независимых испытаний по схеме Бернулли, причем вероятность наступления события А в i — м испытании равна 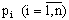 , то вероятность появления события А ровно m раз равна коэффициенту при
, то вероятность появления события А ровно m раз равна коэффициенту при 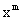 разложения производящей функции
разложения производящей функции 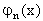 по степеням x :
по степеням x :
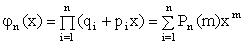 . (13.1.30)
. (13.1.30)
Очевидно, что и в этом случае условие (13.1.27) должно выполняться, что используется при проверке правильности вычисления 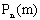 , где
, где 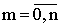 .
.
ПРИМЕР 13.1.20 По цели производится два выстрела. Вероятность попадания при первом выстреле 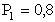 , при втором
, при втором 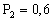 . Найти вероятности событий:
. Найти вероятности событий: 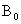 — нет попаданий,
— нет попаданий, 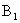 — одно попадание,
— одно попадание, 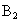 — два попадания.
— два попадания.
Решение. Эта задача может быть решена непосредственно с использованием основных теорем теории вероятностей. Пусть 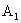 — попадание при первом выстреле,
— попадание при первом выстреле, 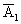 — промах,
— промах, 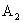 — попадание при втором выстреле,
— попадание при втором выстреле, 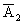 — промах.
— промах.
Тогда 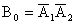 ;
; 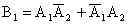 ;
; 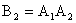 .
.
Имеем
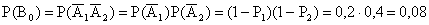 ,
,
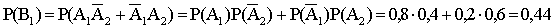 ,
,
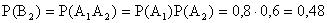 .
.
Проверка
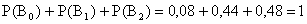 ,
,
.
Второй способ. Обозначим
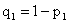 ,
,
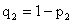 ,
,
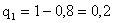 ,
,
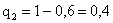 .
.
Имеем схему Бернулли с изменением условий. Составим производящую функцию:
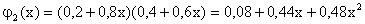 .
.
Отсюда: 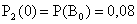 ;
; 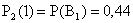 ;
; 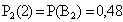 .
.
Получили те же результаты.
Перейдем теперь к рассмотрению предельных теорем в схеме Бернулли.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >