Пусть событие А может наступить при условии появления одного из несовместных событий 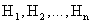 , образующих полную группу. События
, образующих полную группу. События 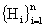 назовем гипотезами. Пусть известны вероятности гипотез
назовем гипотезами. Пусть известны вероятности гипотез 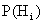 и условные вероятности
и условные вероятности 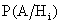 . Чему равна вероятность
. Чему равна вероятность 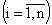
ТЕОРЕМА 13.1.6. Вероятность события А, которое может наступить вместе с одной из гипотез 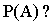 , равна сумме произведений вероятности каждой из гипотез на соответствующую ей условную вероятность события А:
, равна сумме произведений вероятности каждой из гипотез на соответствующую ей условную вероятность события А:
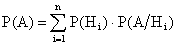 . (13.1.23)
. (13.1.23)
Формулу (13.1.23) называют формулой полной вероятности.
Доказательство: Так как 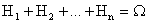 ,
, 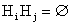 при
при 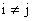 , то событие А можно представить в виде следующей суммы попарно несовместных событий:
, то событие А можно представить в виде следующей суммы попарно несовместных событий: 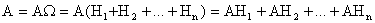 .
.
Используя аксиому A3 и формулу (13.1.2), получим 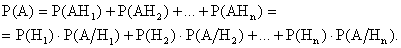
Пусть в результате испытания событие А наступило. Поставим задачу: определить, как изменились ( в связи с тем, что событие А уже наступило) вероятности гипотез, то есть будем искать условные вероятности 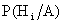
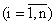 .
.
По теореме умножения имеем
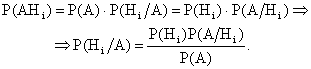
Заменив 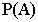 по формуле (13.1.23), окончательно получим
по формуле (13.1.23), окончательно получим
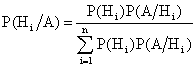 ,
, 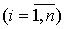 . (13.1.24)
. (13.1.24)
Формула Байеса
Формулу (13.1.24) называют формулой Байеса.
Формулы Байеса позволяют по априорным (известным до испытания) вероятностям найти апостериорные (вычисленные после испытания) вероятности , если известен результат испытания (событие А наступило).
ПРИМЕР 13.1.17 В пирамиде 5 винтовок, две из них снабжены оптическим прицелом. Вероятность поразить мишень при выстреле из винтовки с оптическим прицелом равна 0,9, а для винтовки без оптического прицела – 0,7.
Требуется:
- Найти вероятность поражения мишени, если стрелок произвел один выстрел из наудачу взятой винтовки.;
- Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: мишень поражена из винтовки с оптическим прицелом или без него?
Решение . Введем гипотезы:
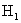 — винтовка с оптическим прицелом;;
— винтовка с оптическим прицелом;;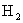 — винтовка без оптического прицела;
— винтовка без оптического прицела;
А – цель поражена при одном выстреле.
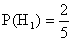 ;
;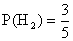 ;
;
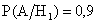 ;
;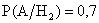 .
.
1) По формуле полной вероятности найдем: 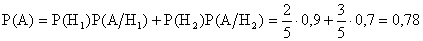 .
.
2) По формуле Байеса найдем вероятности гипотез после испытания:
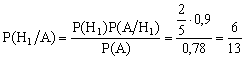 ;
; 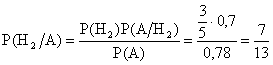 .
.
Так как 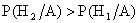 , то более вероятно, что цель поражена из винтовки без оптического прицела.
, то более вероятно, что цель поражена из винтовки без оптического прицела.
Знание основных теорем и формул теории вероятностей позволяет по известным вероятностям элементарных событий находить вероятности сложных событий, что имеет важное практическое значение.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >