Известно, что нормально распределенные случайные величины широко распространены на практике. Например, погрешности измерения каких-либо величин распределены по нормальному закону.
Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А.М. Ляпуновым в центральной предельной теореме.
В грубой формулировке она выглядит так: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.
Более точная формулировка теоремы:
Пусть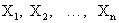 
— независимые случайные величины с математическими ожиданиями 
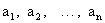и дисперсиями 
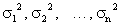, причем
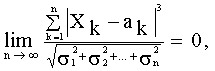
то при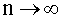 
закон распределения случайной величины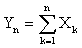 
неограниченно приближается к нормальному.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
