ОПРЕДЕЛЕНИЕ 11.1.10 Дифференциальное уравнение первого порядка называется линейным, если оно линейно (то есть первой степени) относительно искомой функции и ее производной.
Общий вид линейного уравнения
![]() , (11.1.12)
, (11.1.12)
где ![]() и
и ![]() непрерывные функции в некотором промежутке.
непрерывные функции в некотором промежутке.
Если правая часть уравнения ![]() , то уравнение называется линейным однородным, в противном случае оно называется неоднородным. Однородное уравнение имеет вид
, то уравнение называется линейным однородным, в противном случае оно называется неоднородным. Однородное уравнение имеет вид
![]() . (11.1.13)
. (11.1.13)
Уравнение (11.1.13) не требует специального рассмотрения, поскольку оно является уравнением с разделяющимися переменными.
Произведем в уравнении (11.1.12) замену функции, положив ![]() .
.
Тем самым вместо ![]() в качестве искомой функции введем новую функцию, например,
в качестве искомой функции введем новую функцию, например, ![]() . Поэтому вторую функцию
. Поэтому вторую функцию ![]() можно рассматривать как вспомогательное и выбирать его по своему усмотрению. Это и будет сделано в дальнейшем (будем считать, что
можно рассматривать как вспомогательное и выбирать его по своему усмотрению. Это и будет сделано в дальнейшем (будем считать, что ![]() и
и ![]() дифференцируемые функции).
дифференцируемые функции).
Вычислим ![]() и подставим выражения
и подставим выражения ![]() и
и ![]() через
через ![]() и
и ![]() в уравнение (1). Так как
в уравнение (1). Так как ![]() , то уравнение (11.1.12) примет вид
, то уравнение (11.1.12) примет вид
![]() . (11.1.14)
. (11.1.14)
Пользуясь тем, что функция ![]() может быть выбрано произвольно, выберем ее так, чтобы выражение, содержащееся в скобках, обращалось в нуль, то есть потребуем, чтобы
может быть выбрано произвольно, выберем ее так, чтобы выражение, содержащееся в скобках, обращалось в нуль, то есть потребуем, чтобы ![]() . Это уравнение с разделяющимися переменными. Разделив переменные, получим
. Это уравнение с разделяющимися переменными. Разделив переменные, получим ![]() , откуда, интегрируя, имеем:
, откуда, интегрируя, имеем: 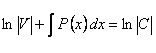
или ![]() .
.
Так как ищем частное решение, можно положить ![]() , тогда
, тогда
![]() . (11.1.15)
. (11.1.15)
Подставив выражение ![]() в уравнение (3), получим для
в уравнение (3), получим для ![]() уравнение с разделяющимися переменными
уравнение с разделяющимися переменными
![]()
![]()
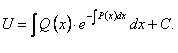 ;(11.1.16)
;(11.1.16)
Формулы (11.1.15) и (11.1.16) дают выражение ![]() и
и ![]() через
через ![]() ; так как нам нужно найти зависимость
; так как нам нужно найти зависимость ![]() от
от ![]() ; а
; а ![]() , то окончательно получим
, то окончательно получим
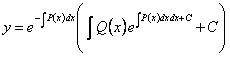 .
.
Это есть общее решение линейного неоднородного уравнения первого порядка, то есть уравнения (11.1.12).
ПРИМЕР 11.1.15 ![]()
Решение.
Здесь ![]() . Сделаем подстановку
. Сделаем подстановку ![]() , отсюда
, отсюда ![]() ; подставляя
; подставляя ![]() и
и ![]() в данное уравнение, получим
в данное уравнение, получим ![]() . Подберем функцию
. Подберем функцию ![]() таким образом, чтобы
таким образом, чтобы ![]() . Это уравнение с разделяющимися переменными. Разделив переменные и, проинтегрировав, получим
. Это уравнение с разделяющимися переменными. Разделив переменные и, проинтегрировав, получим
![]() или
или ![]() при
при ![]()
![]() .
.
Итак, 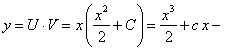 общее решение данного уравнения.
общее решение данного уравнения.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >