Дано однородное дифференциальное уравнение второго порядка
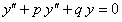 ,(11.1.37)
,(11.1.37)
где 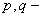 постоянные действительные числа. Чтобы найти его общее решение, достаточно найти два линейно независимых частных решения.
постоянные действительные числа. Чтобы найти его общее решение, достаточно найти два линейно независимых частных решения.
Частное решение ищем в виде:
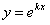 ,(11.1.38)
,(11.1.38)
где 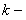 постоянная, тогда
постоянная, тогда 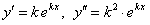 .
.
Подставляя полученные выражения производных и функции в уравнение (11.1.37), находим 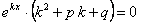 .
.
Так как 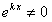 для любого
для любого 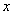 , то
, то
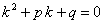 .(11.1.39)
.(11.1.39)
Уравнение (11.1.39) называется характеристическим уравнением по отношению к уравнению (11.1.37).
Характеристическое уравнение есть квадратное уравнение относительно 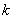 .
.
1. Корни характеристического уравнения действительные и различные. Эти корни обозначим через 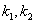 и
и 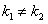 . В этом случае частными решениями будет
. В этом случае частными решениями будет 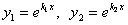 .
.
Эти решения линейно независимы, так как
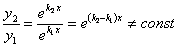 .
.
Тогда общее решение имеет вид: 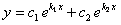 ,
, 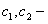 постоянные.
постоянные.
ПРИМЕР 11.1.25 Дано дифференциальное уравнение 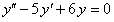 . Требуется найти его общее решение.
. Требуется найти его общее решение.
Решение.
Характеристическое уравнение имеет вид 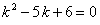 , его корнями являются числа
, его корнями являются числа 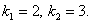 Тогда общим решением будет функция
Тогда общим решением будет функция 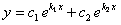 .
.
2. Корни характеристического уравнения комплексные. Так как комплексные корни являются комплексно-сопряженными, то
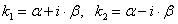 , где
, где 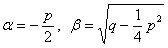 .
.
Частные решения можно записать в виде
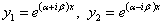 .(11.1.40)
.(11.1.40)
Напишем комплексные решения (11.1.40) в виде суммы, выделяя действительные мнимые части:
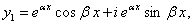
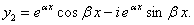
Согласно свойству решений дифференциального уравнения (11.1.37) частными решениями будут функции 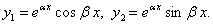
Функции 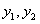 линейно зависимы, тогда функция
линейно зависимы, тогда функция
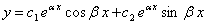 будет общим решением уравнения (11.1.37), где
будет общим решением уравнения (11.1.37), где 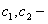 произвольные постоянные.
произвольные постоянные.
ПРИМЕР 11.1.26 Найти общее решение дифференциального уравнения 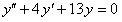 .
.
Решение.
Составляем его характеристическое уравнение
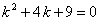 , находим его корни
, находим его корни 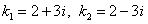 . Тогда общее решение есть
. Тогда общее решение есть 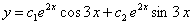 .
.
3. Корни характеристического уравнения действительные и равные.
В этом случае 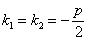 так как
так как 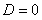 .
.
Первое частное решение 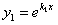 получается на основании предыдущих рассуждений.
получается на основании предыдущих рассуждений.
Второе частное решение ищем в виде 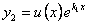 , где
, где 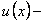 неизвестная функция, подлежащая определению.
неизвестная функция, подлежащая определению.
Дифференцируя 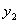 , найдем
, найдем
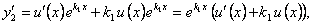
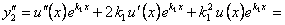
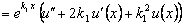 .
.
Подставляя выражения производных функции 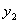 в уравнение (11.1.37), получаем:
в уравнение (11.1.37), получаем: 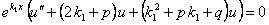 , учитывая, что
, учитывая, что
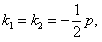
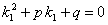 находим, что
находим, что 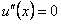 . Интегрируя последнее уравнение, получим
. Интегрируя последнее уравнение, получим 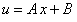 . Полагая, что
. Полагая, что 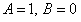 , имеем
, имеем 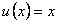 .
.
Таким образом, в качестве второго частного решения можно взять 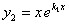 .
.
Тогда функция 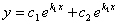 будет общим решением уравнения (1), где
будет общим решением уравнения (1), где 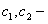 произвольные постоянные.
произвольные постоянные.
ПРИМЕР 11.1.27 Найти общее решение дифференциального уравнения 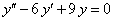 .
.
Решение.
Составим характеристическое уравнение 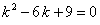 . Найдем его корни:
. Найдем его корни: 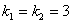 . Тогда
. Тогда 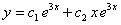 будет общим решением этого уравнения.
будет общим решением этого уравнения.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >