ОПРЕДЕЛЕНИЕ 11.1.14 Дифференциальное уравнение второго порядка называется линейным, если оно линейно относительно искомой функции и ее производных 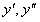, то есть

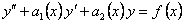,    (11.1.18)

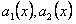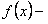где и заданные непрерывные функции в заданном интервале.

Задача Коши для дифференциального уравнения (11.1.18) имеет единственное решение в интервале непрерывности функци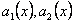и и .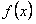

Если 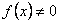, то уравнение называется линейным неоднородным или уравнением с правой частью. Если же 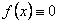, то уравнение (11.1.18) имеет вид

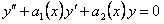(11.1.19)

и называется линейным однородным.

Онлайн помощь

Изучим свойства решений уравнения (11.1.19). Эти свойства сформулируем в виде теорем.

ТЕОРЕМА 11.1.5 Если 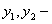два решения линейного однородного уравнения второго порядка (11.1.19), то 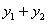также решение этого уравнения.

Доказательство.

Функции y₁y₂ являются решением уравнения (11.1.19), а

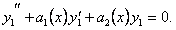(11.1.20)

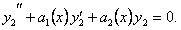(11.1.21)

Подставляя в уравнение (11.1.19) сумму 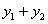и учитывая равенства (11.1.20), (11.1.21), получаем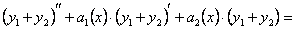

.

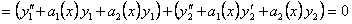Отсюда следует, что 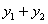является решением уравнения (11.1.19).

ТЕОРЕМА 11.1.6 Если 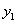является решением уравнения и 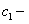постоянная, то 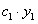также является его решением.

Доказательство. Подставляя в уравнение (11.1.19) произведение 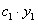, получим: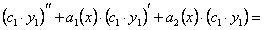

.

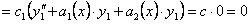Отсюда следует, что c₁*Y₁ является решением уравнения (11.1.19).

ТЕОРЕМА 11.1.7 Если комплексно-значная функция 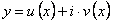является решением уравнения (11.1.19), то функции 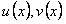также являются  решениями этого уравнения.

Доказательство. Действительно, подставляя функцию 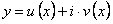в уравнение (11.1.19), имеем

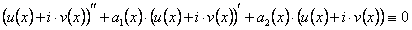
или  .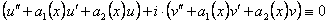

Но комплексно-значная функция равна нулю тогда и только тогда, когда равны нулю ee действительная и мнимая части, то есть

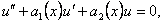
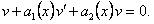
Отсюда следует, что функции 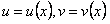являются решениями уравнения (11.1.19).

Следствие. Если 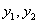являются решениями уравнения (11.1.19) и 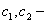постоянные, то 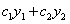является также его решением.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >