Прежде чем давать определение однородного дифференциального уравнения, введем понятие об однородных функциях.
ОПРЕДЕЛЕНИЕ 11.1.8 Функция двух переменных 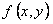 называется однородной функцией порядка
называется однородной функцией порядка 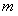 в области
в области 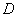 , если при любом
, если при любом 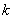 выполняется следующее равенство
выполняется следующее равенство
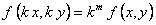 .
.
ПРИМЕР 11.1.12 Функция 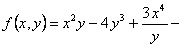 однородная функция третьего порядка, так как
однородная функция третьего порядка, так как
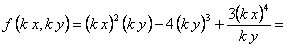
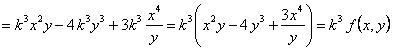 .
.
ПРИМЕР 11.1.13 Функция 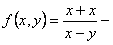 однородная функция нулевого порядка
однородная функция нулевого порядка 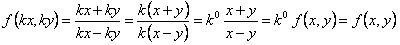 .
.
Таким образом, для функции выполняется равенство 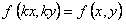 . Отсюда следует, что функция
. Отсюда следует, что функция 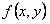 называется однородной функцией нулевого порядка, если при умножении аргументов
называется однородной функцией нулевого порядка, если при умножении аргументов 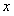 и
и 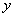 на произвольный параметр
на произвольный параметр 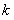 значения функции не изменяются.
значения функции не изменяются.
Отношение двух однородных функций одной переменной и того же порядка однородности является однородной функцией нулевой степени.
Однородная функция нулевого порядка может быть записана в виде
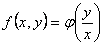 . Действительно, пусть
. Действительно, пусть 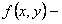 однородная функция нулевого порядка. Так как параметр
однородная функция нулевого порядка. Так как параметр 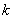 произвольный, то положим
произвольный, то положим 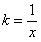 ; тогда
; тогда 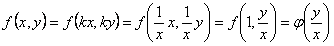 . Теперь можно дать определение однородного дифференциального уравнения относительно
. Теперь можно дать определение однородного дифференциального уравнения относительно 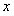 и
и 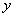 .
.
ОПРЕДЕЛЕНИЕ 11.1.9 Дифференциальное уравнение
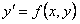 (11.1.8)
(11.1.8)
называется однородным, если 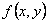 является однородной функцией нулевого порядка.
является однородной функцией нулевого порядка.
Однородное уравнение можно привести к уравнению с разделяющимися переменными подстановкой
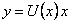 (11.1.9)
(11.1.9)
где 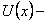 новая дифференцируемая искомая функция. Дифференцируя (11.1.9), получим
новая дифференцируемая искомая функция. Дифференцируя (11.1.9), получим 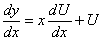 . Подставим выражения
. Подставим выражения 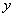 и
и 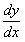 в уравнение (11.1.8), тогда
в уравнение (11.1.8), тогда 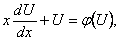 откуда
откуда 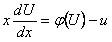 или
или  ,
, 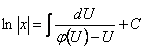 , если
, если 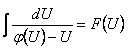 , то
, то 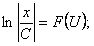
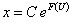 или
или 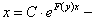 общий интеграл однородного уравнения.
общий интеграл однородного уравнения.
ПРИМЕР 11.1.13 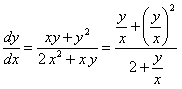
Решение.
Сделаем подстановку: 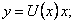
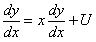 ; подставляя в уравнение, получим
; подставляя в уравнение, получим
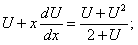
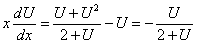 , разделив переменные, имеем
, разделив переменные, имеем 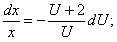
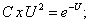
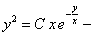 общий интеграл.
общий интеграл.
Уравнение вида
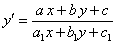 (11.1.10)
(11.1.10)
приводится к однородному, если 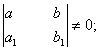 приводится к уравнению с разделяющимися переменными, если
приводится к уравнению с разделяющимися переменными, если 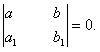
Рассмотрим каждый случай отдельно.
1. Пусть 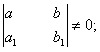 введем новые переменные
введем новые переменные
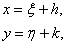 (11.1.11)
(11.1.11)
где 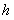 и
и 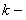 пока не известные постоянные. Найдем
пока не известные постоянные. Найдем 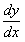 из (11.1.11). Подставляя выражения
из (11.1.11). Подставляя выражения 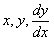 в данное уравнение, получим
в данное уравнение, получим
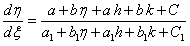 ; выберем теперь
; выберем теперь 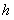 и
и 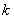 таким образом, чтобы
таким образом, чтобы
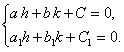 (11.1.12)
(11.1.12)
Тогда 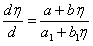 . Это однородное уравнение относительно переменных
. Это однородное уравнение относительно переменных 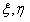 . Решая это уравнение, получим
. Решая это уравнение, получим 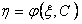 , но
, но 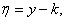
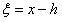 ,
, 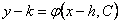 . Значения
. Значения 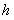 и
и 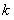 находим из системы (11.1.10);
находим из системы (11.1.10);
она совместна, так как определитель этой системы 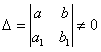 .
.
2. Пусть теперь 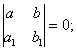
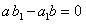 . Отсюда
. Отсюда 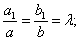
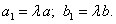 Подставляя значения
Подставляя значения 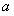 и
и 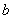 в уравнение (11.1.10), получим
в уравнение (11.1.10), получим
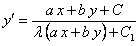 .
.
Для разделения переменных введем новую функцию 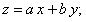 отсюда
отсюда 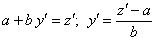 ;
; 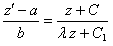 . Это уравнение есть уравнение с разделяющимися переменными.
. Это уравнение есть уравнение с разделяющимися переменными.
ПРИМЕР 11.1.14 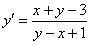 ;
;
Решение.
Проверим 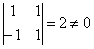 .
.
Введем новые переменные 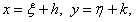
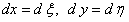 ; уравнение примет вид
; уравнение примет вид
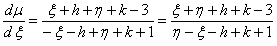 .
.
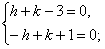 отсюда
отсюда 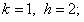
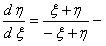 это однородное уравнение.
это однородное уравнение.
Сделаем подстановку 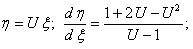
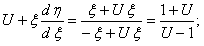
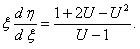
Разделим переменные и проинтегрируем полученное уравнение:
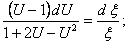
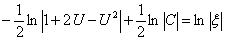 ;
;
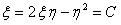 .
.
Или возвращаясь к прежним переменны x и y, получим
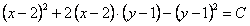 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >