В лабораторной работе №1 в результате первичной обработки исходных данных получено эмпирическое распределение (табл. 14.2.3) и по данным этой таблицы построен полигон относительных частот. Относительные частоты иногда называют эмпирическими вероятностями. Из визуального наблюдения полигона можно сделать один из следующих выводов:

Гипотеза : Генеральная совокупность распределена по нормальному закону;

Гипотеза : Генеральная совокупность распределена по

показательному закону;

Гипотеза : Генеральная совокупность распределена по равномерному закону.

Гипотеза .

Для того, чтобы при заданном уровне значимости ( доверительная вероятность, то есть вероятность принять верную гипотезу; это вероятность отвергнуть верную гипотезу), проверить гипотезу о нормальном распределении генеральной совокупности надо:

1. Вычислить (лабораторная работа № 2).

2. Вычислить теоретические вероятности . Поскольку плотность распределения для нормального закона есть

. (14.2.12)

Тогда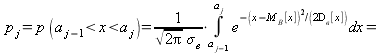

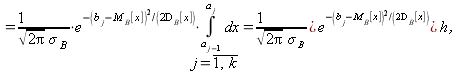(14.2.13)

где границы частичных интервалов;

середина го частичного интервала;

длина частичного интервала (см. формулу (14.2.2)).

3. Составим сводную таблицу на основе данных табл. 14.2.3 и рассчитанных теоретических вероятностей:

Таблица 14.2.6

			…		…
			…		…		эмпирические вероятности
			…		…		теоретические вероятности

4. Оценку отклонения эмпирических вероятностей от теоретических вероятностей производим с помощью критерия Пирсона :

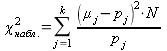. (14.2.14)

5. По таблице критических точек распределения (приложение 4) по заданному уровню значимости и числу степеней свободы ( количество подынтервалов) находим критическое значение правосторонней критической области.

Правило 14.2.1 Если , тогда нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности (то есть эмпирические и теоретические частоты различаются незначимо (случайно).

Правило 14.2.2 Если , тогда гипотезу отвергаем.

Гипотеза .

Для того, чтобы при заданном уровне значимости , проверить гипотезу о показательном распределении генеральной совокупности надо:

1. Вычислить (лабораторная работа № 1). Принять в качестве оценки параметра показательного распределения величину, обратную выборочной средней:

. (14.2.15)

2. Вычислить теоретические вероятности . Поскольку плотность распределения для показательного (экспоненциального) закона есть

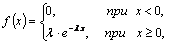(14.2.16)

тогда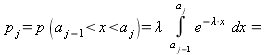

,

где границы частичных интервалов;

вычисляем по формуле (14.2.15).

3. Составим сводную таблицу на основе данных табл. 14.2.3 и рассчитанных теоретических вероятностей (см. табл. 14.2.6).

4. Оценку отклонения эмпирических вероятностей от теоретических вероятностей производим с помощью критерия Пирсона (формула (14.2.14)).

5. По таблице критических точек распределения по заданному уровню значимости и по числу степеней свободы ( количество подынтервалов) находим критическое значение правосторонней критической области (см. Приложение 4).

Далее анализируем в соответствии с правилами 14.2.1 и 14.2.2 (для предыдущей гипотезы).

Гипотеза .

Для того, чтобы при заданном уровне значимости , проверить гипотезу о равномерном распределении генеральной совокупности надо:

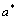1. Оценить параметры и концы интервала, в котором наблюдались возможные значения , по формулам (через и 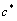обозначены оценки параметров):

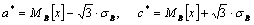. (14.2.17)

2. Вычислить теоретические частоты . Поскольку плотность распределения для равномерного закона есть

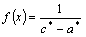, (14.2.18)

тогда

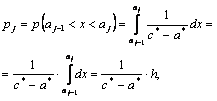(14.2.19)

где границы частичных интервалов;

длина частичных интервалов.

Получили, что все равны одному числу .

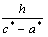3. Составим сводную таблицу на основе эмпирических вероятностей и рассчитанных теоретических вероятностей (см. табл. 14.2.6).

4. Оценку отклонения эмпирических вероятностей от теоретических вероятностей производим с помощью критерия Пирсона (формула (14.2.14)).

5. По таблице критических точек распределения по заданному уровню значимости и по числу степеней свободы ( количество подынтервалов) находим критические значения правосторонней критической области.

Далее анализируем в соответствии с правилами 14.2.1 и 14.2.2 (см. Гипотезу А).

Замечание 14.2.1. После составления таблицы 5 необходимо сделать на одном рисунке два графика: ломаную эмпирических вероятностей и кривую теоретических вероятностей.

Замечание 14.2.2. Здесь же на этом рисунке рекомендуется нанести:

а) ; б) доверительный интервал, построенный для одной из доверительных вероятностей (например, для ); в) интервал, построенный по правилу «3-х сигм».

Замечание 14.2.3. Данный рисунок является наглядным результатом работы, проделанной в Л.Р. 1,2,3.

ПРИМЕР 14.2.3. Используя критерий согласия Пирсона при уровне значимости , проверить гипотезу о нормальном распределении генеральной совокупности.

1) Переносим из лабораторной работы № 1 полигон распределения относительных частот и табл. 14.2.5.

	130,6	290	449,3	608,6	768	927,3	1086,6	1246	1405
	0,06	0,14	0,25	0,18	0,16	0,1	0,05	0,03	0,03

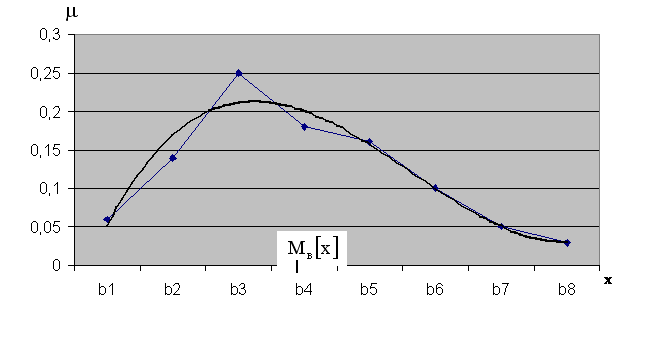
2) Из визуального наблюдения ломаной делаем предположение (ставим гипотезу) о законе распределения генеральной совокупности, то есть ставим гипотезу : выборка распределена по нормальному закону.

3) Вычислим теоретические вероятности . Для этого записываем функцию плотности для нормального закона:

.

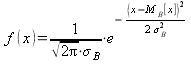Соответственно 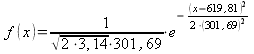или

. Тогда .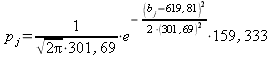

;

;

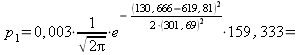
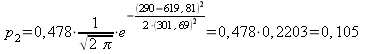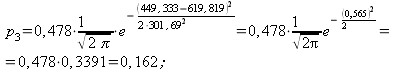
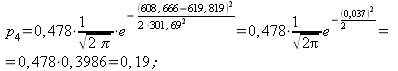
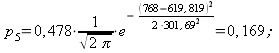
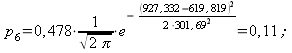
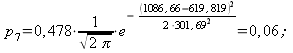
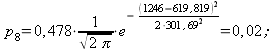
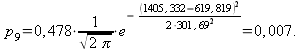
4) Составляем табл. 14.2.7 распределения теоретических вероятностей.

Таблица 14.2.7

	130,6	290	449,3	608,6	768	927,3	1086,6	1246	1405
	0,06	0,14	0,25	0,18	0,16	0,1	0,05	0,03	0,03
	0,05	0,105	0,162	0,19	0,17	0,11	0,06	0,02	0,007

Отметим теоретические вероятности на полигоне относительных частот.

5) Рассчитаем значение критерия .

.

6) Из таблицы «Критические точки распределения » находим соответствующее нашим значениям .

. .

Сравниваем и . Так как , то гипотеза (выборка распределена по нормальному закону) принимается, по правилу 14.2.1.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >