ОПРЕДЕЛЕНИЕ 11.2.14 Уравнение вида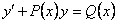 
линейное относительно искомой функции 
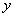и ее производной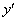 
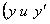входят в уравнение в первых степенях, не перемножаясь между собой) называется линейным.
Если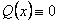 
, то уравнение называется линейным неоднородным, если 
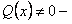линейное однородное.
Общее решение уравнения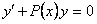 
легко получается разделением переменных:
;
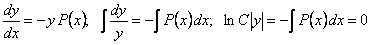
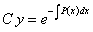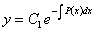, где 
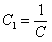.; (11.2.1)
Рассмотрим два способа решения уравнения
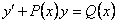.;;(11.2.2)
1. Способ подстановки.
Полагая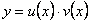 
и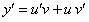 
уравнение (11.2.2) преобразуется в уравнение 
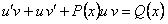или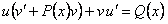 
.
Подберем v таким образом, чтобы уравнение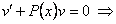 
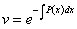, тогда 
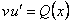или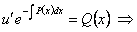 
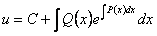. Так как 
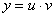, то
.
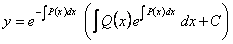Замечание. Если линейное уравнение линейно относительно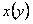 
и x'(y), т.е. имеет вид 
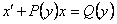, то общее решение его находится подстановкой 
.
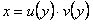ПРИМЕР 11.2.36 Решить уравнение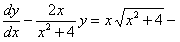 
линейное неоднородное уравнение.
Решение.
Функци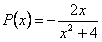и 
и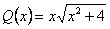 
непрерывны повсюду.
Делаем замену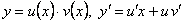 
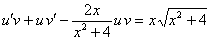или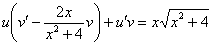 
. Подбираем 
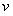таким образом, чтобы 
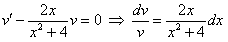или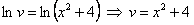 
. Найденное 
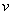подставляем в уравнение 
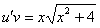получим: 
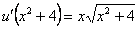или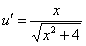 
. Разделяя переменные и интегрируя, имеем
.
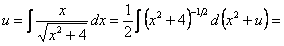
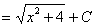Таким образом,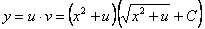 
.
Ответ: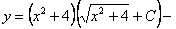 
общее решение.
2. Метод вариации произвольной постоянной.
По методу вариации произвольной постоянной решение уравнения (11.2.2) будем искать, как решение соответствующего однородного уравнения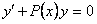 
в виде 
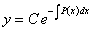, только C будем считать функцией от 
, 
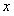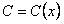. Эта функция должна быть такова, чтобы при подстановке 
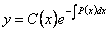и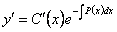 
в уравнение (11.2.2) оно обращалось в тождество.
ПРИМЕР 11.2.37 Найти общее решение уравнения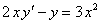 
.
Решение.
Приведем уравнение к виду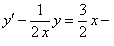 
линейное неоднородное уравнение первого порядка. Решим его по методу вариации произвольной постоянной. Первоначально, решаем однородное уравнение 
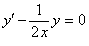. Разделяя переменные, получим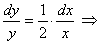 
, 
.
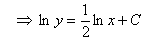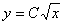По методу вариации общее решение будем искать в виде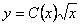 
, 
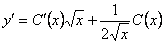. Подставим 
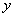и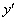 
в данное уравнение.
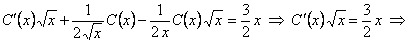
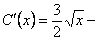интегрируя, получим: 
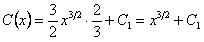. Таким образом, 
.
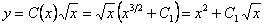Ответ: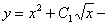 
общее решение.
Примеры и задачи для самостоятельного решения:
Решить уравнения
11.2.38  |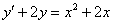
Отв.  |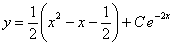
11.2.39  ; |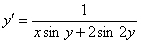
Отв.  |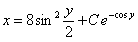
11.2.40  ; |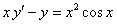
Отв. |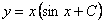
11.2.41 ; |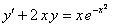
Отв.  |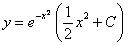
11.2.42  |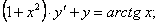
Отв.  |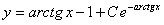
| Найти частное решение уравнений | |
11.2.43  ; |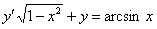
Отв.  |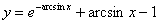
11.2.44  ; |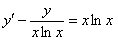
Отв.  |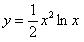
11.2.45  |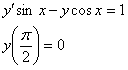
Отв.  |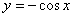
11.2.46 Найти линию, у которой начальная ордината любой касательной на две единицы масштаба меньше абсциссы точки касания.
Отв.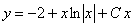 
11.2.47 Найти линию, у которой площадь треугольника, построенного на абсциссе любой точки и начальной ординате касательной в этой точке, есть величина постоянная, равная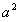 
.
Отв.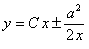 
11.2.48 Точка массой равной m движется прямолинейно, на нее действует сила, пропорциональная времени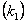 
, прошедшему от момента, когда скорость равнялась нулю. Кроме того, на точку действует сила сопротивления среды, пропорциональная скорости 
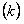. Найти зависимость скорости от времени.
Отв.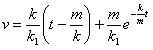 
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
