ОПРЕДЕЛЕНИЕ 11.2.10 Функция 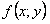 называется однородной
называется однородной 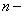 го измерения относительно своих аргументов
го измерения относительно своих аргументов 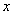 и
и 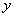 , если для любого значения
, если для любого значения 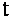 имеет место тождество
имеет место тождество 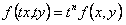 .
.
ОПРЕДЕЛЕНИЕ 11.2.11 Функция 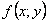 называется однородной нулевого измерения относительно
называется однородной нулевого измерения относительно 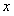 и
и 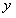 , если для любого
, если для любого 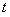 имеет место равенство
имеет место равенство 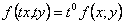 .
.
ОПРЕДЕЛЕНИЕ 11.2.12 Дифференциальное уравнение вида 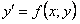 называется однородным относительно
называется однородным относительно 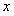 и
и 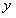 , если
, если 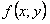 является однородной функцией нулевого измерения.
является однородной функцией нулевого измерения.
ОПРЕДЕЛЕНИЕ 11.2.13 Дифференциальное уравнение 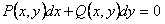 называется однородным, если
называется однородным, если 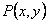 и
и 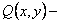 однородные функции одного измерения.
однородные функции одного измерения.
Однородное уравнение может быть приведено к виду 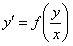 . С помощью подстановки
. С помощью подстановки 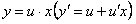 , оно приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции
, оно приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции 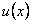 .
.
ПРИМЕР 11.2.18 Найти общее решение уравнения 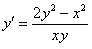 .
.
Решение.
Функция 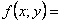
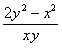 является однородной функцией нулевого измерения, так как
является однородной функцией нулевого измерения, так как 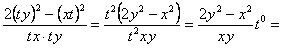
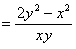 . Значит данное уравнение однородное. Сделаем замену
. Значит данное уравнение однородное. Сделаем замену 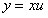 ,
, 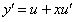 и подставим в уравнение, получим
и подставим в уравнение, получим
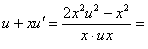
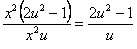 .
.
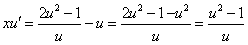 или
или 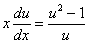 .
.
Разделяя переменные и интегрируя, получим 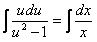 .
.
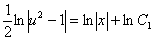 , или
, или 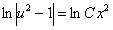 , где
, где 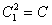 .
.
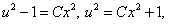 где
где 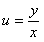 .
.
Возвращаясь к прежней неизвестной функции 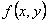 , получаем окончательный ответ
, получаем окончательный ответ 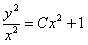 или
или 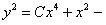 общий интеграл данного уравнения.
общий интеграл данного уравнения.
ПРИМЕР 11.2.19 Найти частное решение уравнения
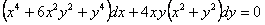 ,
, 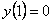 .
.
Решение.
В данном случае 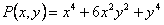 , а
, а 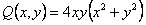 . Обе функции — однородные четвертого измерения. Значит данное уравнение однородное. Введем подстановку
. Обе функции — однородные четвертого измерения. Значит данное уравнение однородное. Введем подстановку 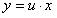
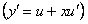 . Тогда уравнение примет вид
. Тогда уравнение примет вид
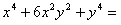
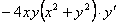 ,
, 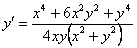 ;
;
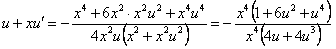
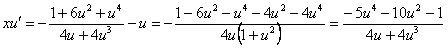
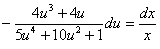 интегрируя, получим
интегрируя, получим
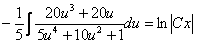 ;
; 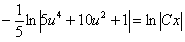 ;
;
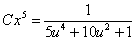 . Возвращаясь к прежней неизвестной и используя начальные условия, получим
. Возвращаясь к прежней неизвестной и используя начальные условия, получим 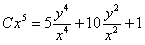 ,
,
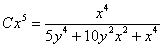 ,
, 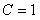 . Сокращая на
. Сокращая на 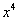 , окончательно имеем
, окончательно имеем
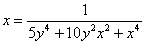 или
или 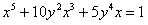 .
.
ПРИМЕР 11.2.20 Составить уравнение кривой, проходящей через точку (1,1), если известно, что произведение абсциссы любой точки кривой на угловой коэффициент касательной к кривой в этой точке равно удвоенной сумме координат точки.
Решение.
Пусть 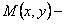 точка касания, тогда угловой коэффициент касательной, проведенной в точке
точка касания, тогда угловой коэффициент касательной, проведенной в точке 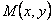 равен
равен 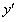 . По условию задачи
. По условию задачи 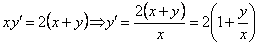 . Получили однородное уравнение. Сделаем подстановку
. Получили однородное уравнение. Сделаем подстановку 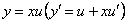

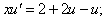
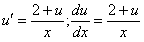
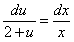 . Интегрируя, получим
. Интегрируя, получим 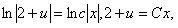
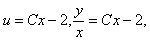 но
но 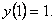
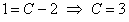 .
.
Итак, 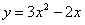 . Это уравнение параболы с вершиной в точке
. Это уравнение параболы с вершиной в точке 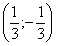 и пересекающая ось
и пересекающая ось 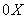 в точках
в точках 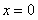 и
и 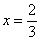 .
.
Задачи и примеры для самостоятельного решения
| Решить уравнения | ||
11.2.21 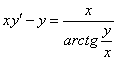 |
Отв.: 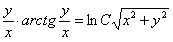 |
|
11.2.22 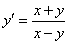 |
Отв.: 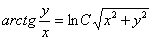 |
|
11.2.23 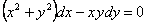 |
Отв.: 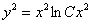 |
|
| Найти частные решения дифференциальных уравнений | ||
11.2.24 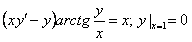 |
Отв.: 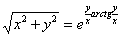 |
|
11.2.25 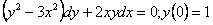 |
Отв.: 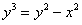 |
|
11.2.26 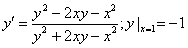 |
Отв.: 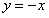 |
11.2.27 Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания.
Ответ: 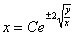 .
.
11.2.28 Найти линию, у которой начальная ордината любой касательной равна соответствующей поднормали.
Ответ: 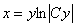 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >