Пусть составляющие X и Y дискретны и их возможные значения:
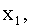
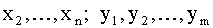 .
.
Условным распределением составляющей X при 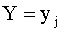 называют совокупность условных вероятностей
называют совокупность условных вероятностей 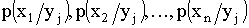 , вычисленных в предположении, что событие
, вычисленных в предположении, что событие 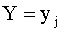 (j имеет одно и то же значение при всех значениях X) уже наступило. Аналогично определяется условное распределение составляющей Y.
(j имеет одно и то же значение при всех значениях X) уже наступило. Аналогично определяется условное распределение составляющей Y.
Условные вероятности вычисляются по формулам
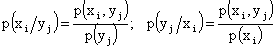 .
.
Пусть 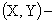 непрерывная двумерная случайная величина с плотностью распределения
непрерывная двумерная случайная величина с плотностью распределения 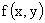 .
.
Условной плотностью 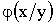 распределения составляющей X при заданном значении
распределения составляющей X при заданном значении 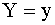 называют
называют
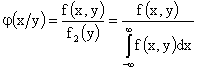 .
.
Аналогично определяется условная плотность распределения составляющей Y при заданном значении 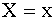
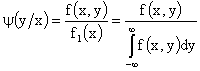 .
.
Запишем последние формулы в виде
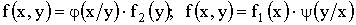
Если X и Y — независимые случайные величины, то 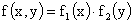 , то есть для независимых случайных величин условные плотности распределения равны их безусловным плотностям
, то есть для независимых случайных величин условные плотности распределения равны их безусловным плотностям 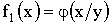 ;
; 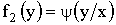 .
.
Условным математическим ожиданием одной из случайных величин, входящих в систему (X,Y), называется ее математическое ожидание,вычисленное в предположении, что другая случайная величина приняла определенное значение, то есть найденное на основе условного закона распределения.
Для дискретных величин
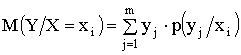 ,
,
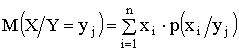 .
.
Для непрерывных величин
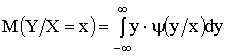 ,
,
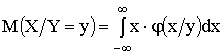 .
.
Условное математическое ожидание 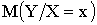 есть функция от x:
есть функция от x: 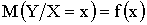 , которую называют функцией регрессии Y на X. Аналогично функция регрессии Y на X — это функция
, которую называют функцией регрессии Y на X. Аналогично функция регрессии Y на X — это функция 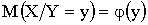 . Графики этих функций называются линиями регрессии или «кривыми регрессии».
. Графики этих функций называются линиями регрессии или «кривыми регрессии».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.55. Задана дискретная двумерная случайная величина .
| Y\X | 2 | 5 | 8 |
| 0,4 | 0,15 | 0,30 | 0,35 |
| 0,8 | 0,05 | 0,12 | 0,03 |
Найти: а) условный закон распределения составляющей X при условии Y=0,4 ;
б) условный закон распределения Y при условии x=5.
Решение. Найдем условные вероятности
а) 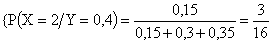 ;
;
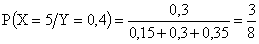 ;
;
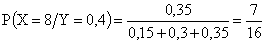 .
.
Тогда искомый условный закон распределения :
| X | 2 | 5 | 8 |
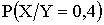 |
3/16 | 3/8 | 7/16 |
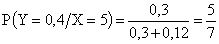 ;
;
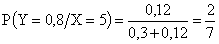 .
.
| Y | 0,4 | 0,8 |
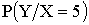 |
5/7 | 2/7 |
ПРИМЕР 13.2.56.
| X\Y | 0 | 3 | 5 |
| 1 | 0 | 0,05 | 0,1 |
| 5 | 0,1 | 0,1 | 0,15 |
| 12 | 0,1 | 0,15 | 0,25 |
Построить линии регрессии Y на X.
Решение. Найдем условные законы Y при X=1, X=5 и X=12.
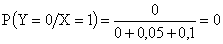 ,
,
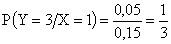 ,
,
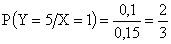 .
.
| Y | 0 | 3 | 5 |
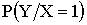 |
0 | 1/3 | 2/3 |
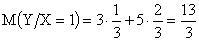 ,
,
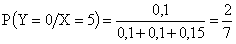 ,
,
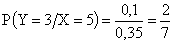 ,
,
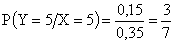 .
.
| Y | 0 | 3 | 5 |
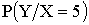 |
2/7 | 2/7 | 3/7 |
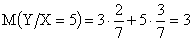 ,
,
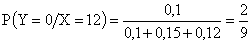 ,
,
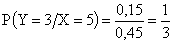 ,
,
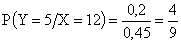 .
.
| Y | 0 | 3 | 5 |
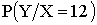 |
2/9 | 1/3 | 4/9 |
Линия регрессии
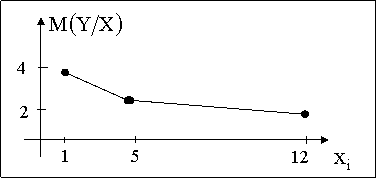
ПРИМЕР 13.2.57. Задана плотность совместного распределения непрерывной двумерной случайной величины (X,Y).
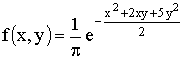 .
.
Найти: а) плотности распределения составляющих; б) условные плотности распределения составляющих.
Решение. а) Найдем плотность распределения составляющей 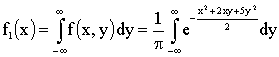 :
:
Вынесем за знак интеграла множитель 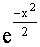 , не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата, тогда
, не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата, тогда 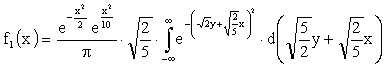
.
Учитывая, что интеграл Пуассона 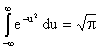 , получаем
, получаем 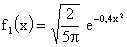 .
.
Аналогично найдем плотность распределения составляющей Y: 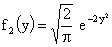 .
.
б) Найдем условные плотности распределения составляющих.
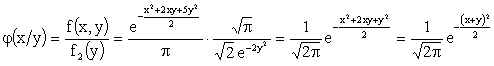 ;
;
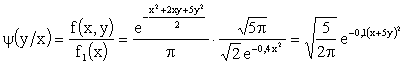 .
.
ПРИМЕР 13.2.58. Задана плотность распределения двумерной случайной величины (X,Y) : 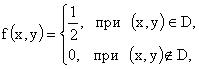 , где
, где 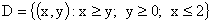 .
.
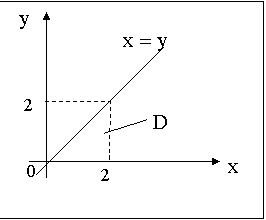
Найти линию регрессии СВ X на СВ Y.
Решение. Найдем условную плотность распределения X на Y.
Из области D видно, что 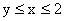
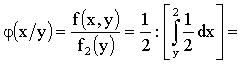 ;
;
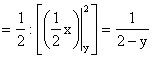 ;
;
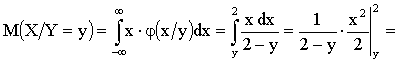 ;
;
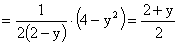 .
.
Примеры и задачи для самостоятельного решения
Решить задачи на условные законы распределения составляющих двумерной случайной величины
3.2.13.1. Задана дискретная двумерная случайная величина
| Y\X | 3 | 6 |
| 10 | 0,25 | 0,10 |
| 14 | 0,15 | 0,05 |
| 18 | 0,32 | 0,13 |
Найти: а) условный закон распределения Y при условии, что X=6; б)построить линию регрессии X на Y.
Отв.:
3.2.13.2. Непрерывная двумерная случайная величина (X,Y) равномерно распределена внутри прямоугольного треугольника с вершинами 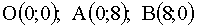 . Найти: а)двумерную плотность вероятности системы; б) плотности и условные плотности распределения составляющих.
. Найти: а)двумерную плотность вероятности системы; б) плотности и условные плотности распределения составляющих.
Отв.:
3.2.13.3. Плотность совместного распределения непрерывной двумерной случайной величины 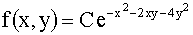 .
.
Найти: а) постоянный множитель C; б) плотность распределения составляющих; в) условные плотности распределения составляющих.
Отв.: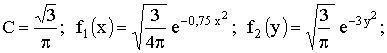 ,
,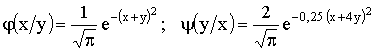
3.2.13.4. Двумерная случайная величина (X,Y) задана плотностью распределения 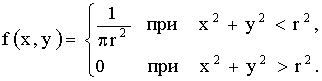 .
.
Найти условные законы распределения вероятностей составляющих.
Отв.: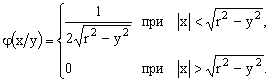 ,
,
3.2.13.5. Плотность совместного распределения непрерывной двумерной случайной величины 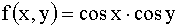 в квадрате
в квадрате 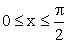 ;
; 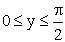 ; вне квадрата
; вне квадрата 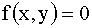 . Доказать, что X и Y — независимые случайные величины. Найти линию регрессии Y на X.
. Доказать, что X и Y — независимые случайные величины. Найти линию регрессии Y на X.
Отв.:
3.2.13.6. Плотность распределения двумерной непрерывной случайной величины 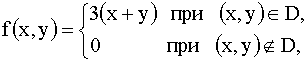
где 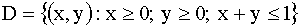 .
.
Найти функцию регрессии X на Y.
Отв.: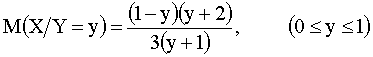
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >