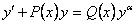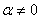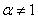ОПРЕДЕЛЕНИЕ 11.2.15 Уравнение вида, где , называется уравнением Бернулли.

Уравнение Бернулли 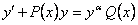(11.2.3)

путем деления его на y^α сводится к линейному ,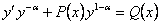

полагая 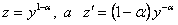, получим 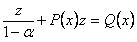или

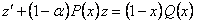. Решая полученное уравнение, находим 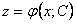, а затем и y, из замены 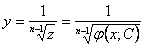. Таким образом, уравнение Бернулли можно сразу решать как линейное подстановкой 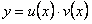не сводя его предварительно к линейному.

Онлайн помощь

ПРИМЕР 11.2.49 Найти общее решение уравнения .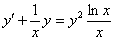

Решение.

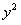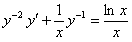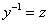
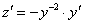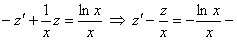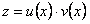
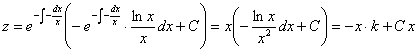Данное уравнение является уравнением Бернулли. Разделим обе части уравнения на и сделаем замену: ; , линейное уравнение. По формуле (5.3) найдем общее решение

, где

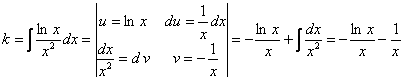, тогда

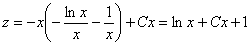, но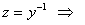

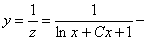общее решение уравнения Бернулли.

ПРИМЕР 11.2.50 Найти общее решение уравнения

Решение.

Данное уравнение является уравнением Бернулли 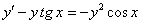. Будем решать его сразу как линейное заменой .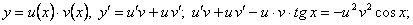

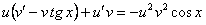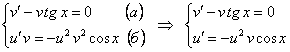
Решаем уравнение (а).

. Найденное 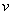подставим в уравнение (б)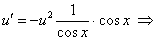

.

.

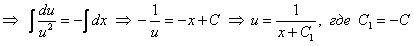Ответ. 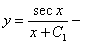общее решение.

Задачи и примеры для самостоятельного решения

Найти общее решение уравнений

11.2.51 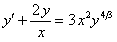;	Отв. .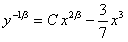
11.2.52 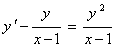;	Отв. .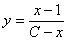
11.2.53 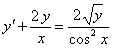;	Отв. .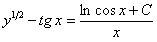
11.2.54 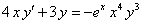;	Отв. .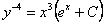
Найти частные решения уравнений
11.2.55 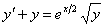;	Отв. .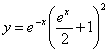
11.2.56 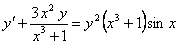;	Отв. .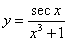

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >