ОПРЕДЕЛЕНИЕ 12.2.14 Функциональный ряд вида
 (12.2.16)
(12.2.16)
называется тригонометрическим рядом.
ПРИМЕР 12.2.27 Разложить в ряд Фурье функцию 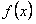 с периодом
с периодом 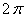 , если
, если 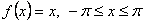 .
.
Решение.
Функция 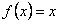 удовлетворяет условиям Дирихле, следовательно, она допускает разложение в ряд Фурье.
удовлетворяет условиям Дирихле, следовательно, она допускает разложение в ряд Фурье.
Находим 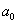 :
:
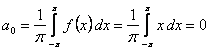 (так как
(так как 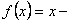 нечетная).
нечетная).
Определим 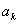 и
и  :
:
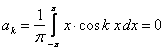
(так как 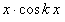 есть функция нечетная как произведение четной функции на нечетную, то определенный интеграл в симметричных пределах интегрирования относительно нуля от нечетной функции равен нулю).
есть функция нечетная как произведение четной функции на нечетную, то определенный интеграл в симметричных пределах интегрирования относительно нуля от нечетной функции равен нулю).
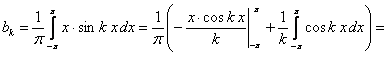

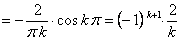 .
.
Таким образом, получаем ряд
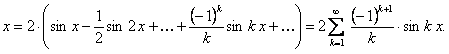
Это равенство имеет место во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равно среднему арифметическому ее пределов справа и слева, то есть равна нулю.
ПРИМЕР 12.2.28 Разложить в ряд Фурье функцию 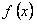 с периодом
с периодом 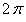 , которая на отрезке
, которая на отрезке 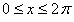 задана равенством
задана равенством 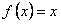 .
.
Решение.
График функции изображен на рис. 12.2.1 Как видно на рис. 12.2.1 функция на отрезке 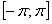 задана двумя формулами
задана двумя формулами

и вычисление коэффициентов ряда Фурье по формулам (12.1.91), (12.1.101), (12.1.103) неудобно, так как в каждом из интегралов интервал интегрирования приходится разбивать на два: от 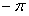 до
до 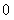 и от
и от 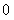 до
до 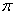 . В то же время на отрезке
. В то же время на отрезке 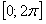 функция гораздо проще, она задается одной формулой
функция гораздо проще, она задается одной формулой 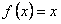 . Поэтому для вычисления коэффициентов ряда Фурье удобнее формулы (12.1.105) при
. Поэтому для вычисления коэффициентов ряда Фурье удобнее формулы (12.1.105) при 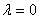 .
.
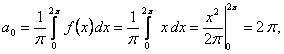

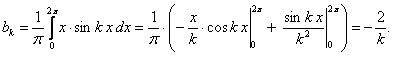
Тогда разложение функции в ряд Фурье будет иметь вид
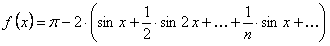 .
.
Этот ряд дает заданную функцию во всех точках, кроме точек разрыва (то есть кроме точек 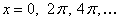 ). В этих точках сумма ряда равна полусумме предельных значений функции
). В этих точках сумма ряда равна полусумме предельных значений функции 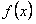 справа и слева, в данном случае числу
справа и слева, в данном случае числу 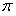 .
.
ПРИМЕР 12.2.29 Разложить в ряд Фурье функцию 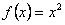 периода
периода 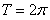
 .
.
Решение.
Данная функция четная. Тогда ее ряд Фурье содержит только косинусы 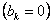 . Вычислим коэффициенты
. Вычислим коэффициенты 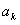 :
:
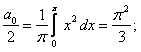
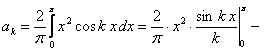
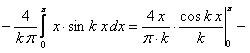
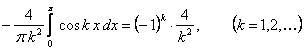 .
.
Таким образом, 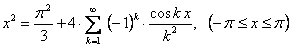 .
.
ПРИМЕР 12.2.30 Разложить в ряд Фурье периодическую функцию 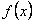 с периодом
с периодом 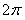 , которая определена следующим образом:
, которая определена следующим образом: 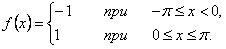
Решение.
Эта функция нечетная. Тогда ее ряд Фурье содержит только синусы 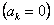 . Вычислим коэффициент
. Вычислим коэффициент 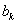 :
:
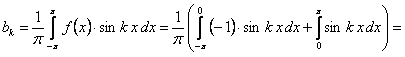
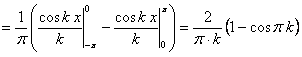 .
.
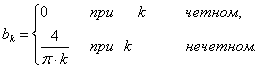
Следовательно, для рассматриваемой функции ряд Фурье имеет вид
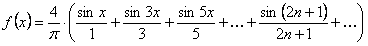 .
.
Это равенство справедливо во всех точках, кроме точек разрыва.
ПРИМЕР 12.2.31 Разложить в ряд Фурье периодическую функцию 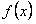 с периодом
с периодом 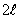 , которая на отрезке
, которая на отрезке 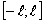 задается равенством
задается равенством
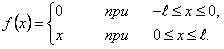
Решение.
Определим коэффициенты Фурье
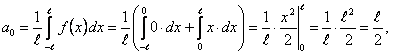
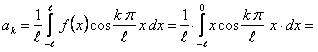
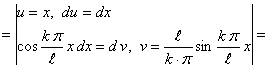
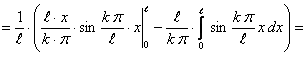
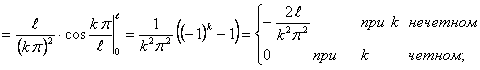
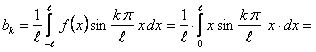

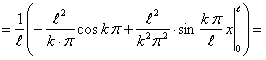

Таким образом, ряд Фурье для этой функции будет иметь вид
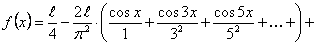
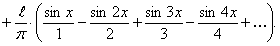
ПРИМЕР 12.2.32 Требуется разложить функцию  на отрезке
на отрезке 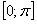 в ряд по синусам.
в ряд по синусам.
Решение.
Продолжая эту функцию нечетным образом, получим
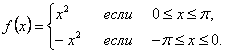

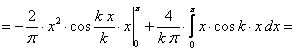
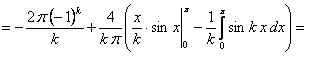
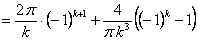 , так что
, так что
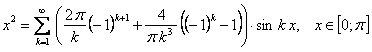 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >