Двумерной называют случайную величину (X,Y), возможные значения которой есть пары чисел (x,y). Составляющие X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, то есть пар чисел 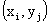 и их вероятностей
и их вероятностей 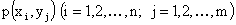 . Обычно закон распределения задают в виде таблицы, называемой матрицей распределения.
. Обычно закон распределения задают в виде таблицы, называемой матрицей распределения.
| Y\X | 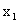 |
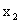 |
… | 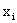 |
… | 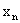 |
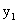 |
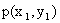 |
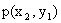 |
… | 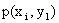 |
… | 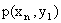 |
| … | … | … | … | … | … | … |
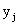 |
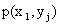 |
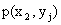 |
… | 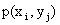 |
… | 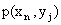 |
| … | … | … | … | … | … | … |
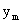 |
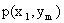 |
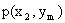 |
… | 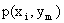 |
… | 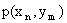 |
Сумма вероятностей, помещенных во всех клетках таблицы, равна единице.
Из данной таблицы закон распределения составляющей СВ X.
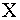 |
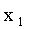 |
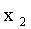 |
… | 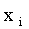 |
… | 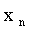 |
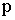 |
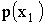 |
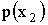 |
… | 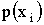 |
… | 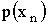 |
где 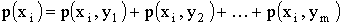 ,
, 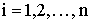 .
.
Аналогично можно найти закон распределения составляющей СВ Y.
Двумерную случайную величину (X,Y) (безразлично, дискретную или непрерывную) можно задать с помощью функции распределения F(x,y), которая определяет вероятность того, что X примет значение, меньшее x, Y — меньшее y.
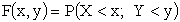 .
.
Свойства функции распределения:
1)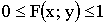 ;
;
2) 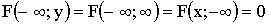 ;
;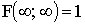
3) 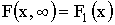 , где
, где 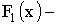 функция распределения составляющей X;
функция распределения составляющей X;
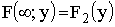 , где функция
, где функция 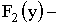 распределения составляющей Y.
распределения составляющей Y.
При помощи функции распределения может быть найдена вероятность
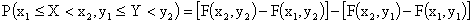 .
.
Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения. Плотностью совместного распределения вероятностей f(x,y) двумерной непрерывной случайной величины (X,Y)
называют вторую смешанную частную производную от функции распределения: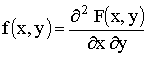 .
.
Свойства плотности распределения:
1) 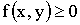 ;
;
2) 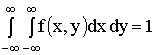 .
.
Плотности распределения
составляющей X — 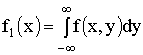 ;
;
составляющей Y — 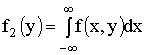 .
.
Вероятность попадания случайной точки (X,Y) в область D определяется по формуле
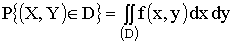 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.49. Два стрелка, независимо друг от друга, делают по одному выстрелу каждый. Случайная величина X — число попаданий первого стрелка, Y — число попаданий второго стрелка. Вероятность попадания при выстреле для первого стрелка 0,7; для второго стрелка — 0,4. Построить матрицу распределения системы случайных величин (X,Y) и законы распределения составляющих X и Y. Найти функцию распределения F(x,y).
Решение. Занесем возможные значения случайных величин X и Y в таблицу
| X\Y | 0 | 1 |
| 0 | 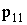 |
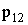 |
| 1 | 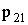 |
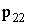 |
 ,
,
 ,
,
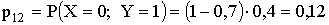 ,
,
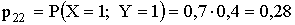 .
.
Итак,
| X\Y | 0 | 1 |
| 0 | 0,18 | 0,12 |
| 1 | 0,42 | 0,28 |
Напишем закон распределения составляющей
| Y | 0 | 1 |
| P | 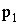 |
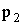 |
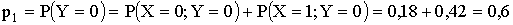 ,
,
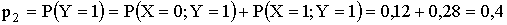 .
.
Тогда
| Y | 0 | 1 |
| P | 0,6 | 0,4 |
Аналогично находится закон распределения составляющей x (складываются вероятности по столбцам).
| x | 0 | 1 |
| P | 0,3 | 0,7 |
Значения функции распределения F(x,y) находим на основании матрицы распределения
| X\Y |  |
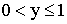 |
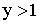 |
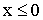 |
0 | 0 | 0 |
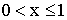 |
0 | 0,18 | 0,18+0,12 |
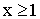 |
0 | 0,18+0,42 | 0,18+0,12+0,42+0,28 |
Окончательно,
| X\Y |  |
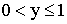 |
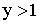 |
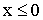 |
0 | 0 | 0 |
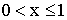 |
0 | 0,18 | 0,3 |
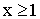 |
0 | 0,6 | 1 |
ПРИМЕР 13.2.50. Задана двумерная плотность вероятности 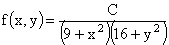 системы (X,Y) двух случайных величин. Найти постоянную C и плотности распределения составляющих системы.
системы (X,Y) двух случайных величин. Найти постоянную C и плотности распределения составляющих системы.
Решение. Воспользуемся свойством 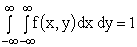 .
.
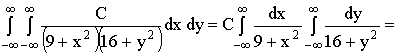
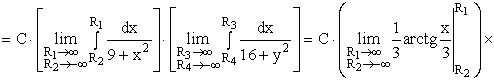
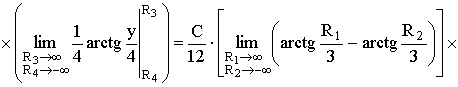
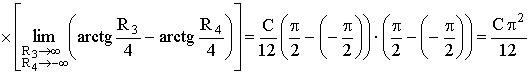
Тогда, 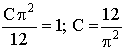 .
.
Найдем плотность распределения 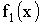 составляющей X
составляющей X
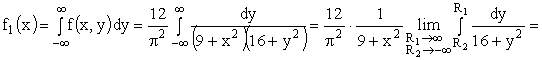
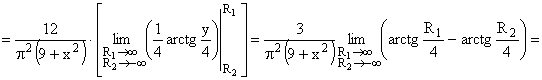
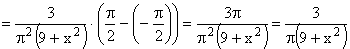
Аналогично можно найти плотность распределения 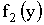 составляющей Y.
составляющей Y.
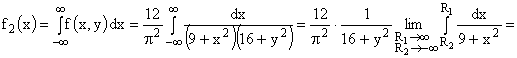
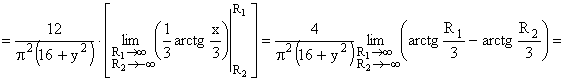
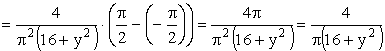
ПРИМЕР 13.2.51. Найти вероятность попадания случайной точки (X,Y) в прямоугольник, ограниченный прямыми 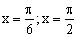 ,
, 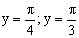 , если известна функция распределения
, если известна функция распределения
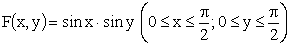 .
.
Решение. Положив 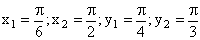 в формуле
в формуле
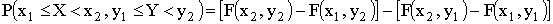 ,
,
получим
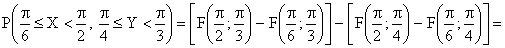
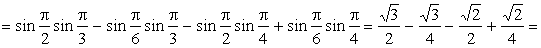
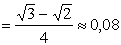
ПРИМЕР 13.2.52 В круге 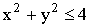 двумерная плотность вероятности
двумерная плотность вероятности 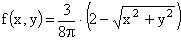 ; вне круга
; вне круга 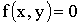 . Найти вероятность попадания случайной точки (x,y) в круг радиуса
. Найти вероятность попадания случайной точки (x,y) в круг радиуса 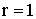 с центром в начале координат.
с центром в начале координат.
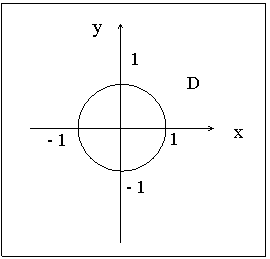
Решение: Пусть область 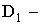 круг радиуса
круг радиуса 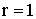 с центром в начале координат, тогда
с центром в начале координат, тогда
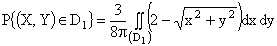 .
.
Перейдем к полярным координатам: 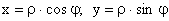
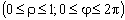
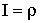
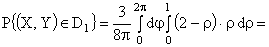
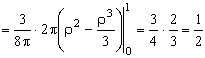 .
.
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулы расчета вероятности для системы двух случайных величин
3.2.11.1. Два игрока, независимо друг от друга, по два раза выбрасывают игральный кубик. Случайная величина X — число выпадений «шестерки» у первого игрока; Y — число выпадений «шестерки» у второго игрока. Построить матрицу распределения системы случайных величин (X,Y) и законы распределения составляющих. Найти функцию распределения F(x,y).
Отв.:
3.2.11.2. Найти вероятность того, что составляющая X двумерной случайной величины примет значение 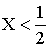 и при этом составляющая Y примет значение
и при этом составляющая Y примет значение 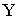 , если известна функция распределения системы
, если известна функция распределения системы 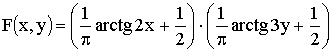 .
.
Отв.: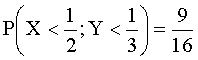
3.2.11.3. Найти вероятность попадания случайной точки (X,Y) в прямоугольник, ограниченный прямыми 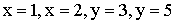 , если известна функция распределения
, если известна функция распределения 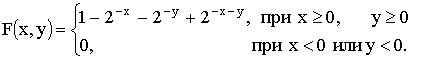 .
.
Отв.: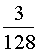
3.2.11.4. Найти плотность распределения системы двух случайных величин по известной функции распределения
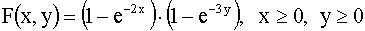 .
.
Отв.: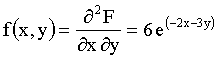
3.2.11.5. Внутри прямоугольника, ограниченного прямыми 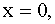
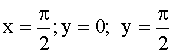 , плотность распределения системы двух случайных величин
, плотность распределения системы двух случайных величин 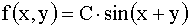 ; вне прямоугольника
; вне прямоугольника 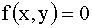 . Найти: а) величину C; б) функцию распределения системы F(x,y).
. Найти: а) величину C; б) функцию распределения системы F(x,y).
Отв.: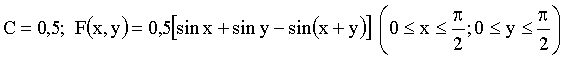
3.2.11.6. Задана двумерная плотность вероятности 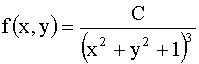 системы случайных величин (X,Y). Найти постоянную C.
системы случайных величин (X,Y). Найти постоянную C.
Указание: Перейти к полярным координатам.
Отв.:
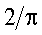
3.2.11.7. В первом квадранте задана функция распределения системы двух случайных величин: 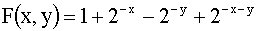 . Найти: а)двумерную плотность распределения системы; б)вероятность попадания случайной точки (X,Y) в треугольник с вершинами
. Найти: а)двумерную плотность распределения системы; б)вероятность попадания случайной точки (X,Y) в треугольник с вершинами 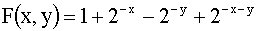 .
.
Отв.: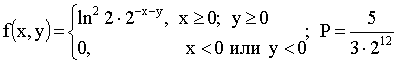
3.2.11.8. Непрерывная двумерная случайная величина (X,Y) распределена равномерно внутри прямоугольника R, ограниченного абсциссами 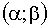 и ординатами
и ординатами 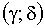 . Найти: а)двумерную плотность вероятности системы; б)плотности распределения составляющих. Определить, зависимы или независимы случайные величины X и Y.
. Найти: а)двумерную плотность вероятности системы; б)плотности распределения составляющих. Определить, зависимы или независимы случайные величины X и Y.
Отв.:
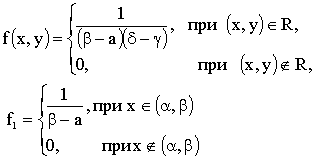
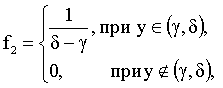 .
.
X и Y независимы,т.к. 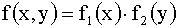 .
.
3.2.11.9. Точка (X,Y), изображающая объект на круглом экране радиолокатора, распределена с постоянной плотностью в пределах круга K радиуса r с центром в начале координат. Записать выражение совместной плотности f(x,y). Найти плотности отдельных величин, входящих в систему 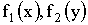 . Найти вероятность того, что расстояние от точки (X,Y) до центра экрана будет меньше
. Найти вероятность того, что расстояние от точки (X,Y) до центра экрана будет меньше 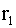 .
.
Отв.: 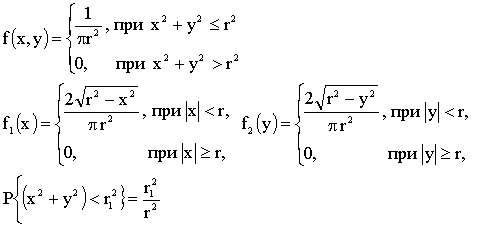
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >