Неравенство Чебышева. Для любой случайной величины X, имеющей математическое ожидание m и дисперсию 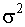 , справедливы неравенства:
, справедливы неравенства:
 или
или 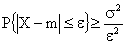 .
.
Теорема Чебышева. Если 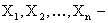 попарно независимые случайные величины с конечными математическими ожиданиями, дисперсии которых ограничены одним и тем же числом
попарно независимые случайные величины с конечными математическими ожиданиями, дисперсии которых ограничены одним и тем же числом 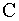 , то есть
, то есть
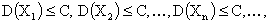 ,
,
то
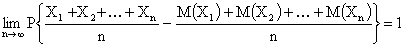 .
.
Если математическое ожидание всех случайных величин равны, то есть 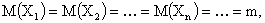
то
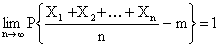 .
.
Замечание. Для случайных величин с равными математическими ожиданиями теорему Чебышева можно записать в виде
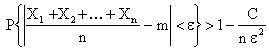 .
.
с равными дисперсиями
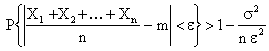 .
.
Теорема Бернулли. Пусть X — число «успехов» в схеме Бернулли с n испытаниями, p — вероятность «успеха» в одном испытании. Тогда для любого 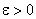 ,
,
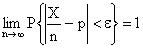 .
.
Замечание 1. Учитывая замечание к теореме Чебышева теорему Бернулли можно записать
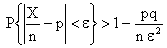 .
.
Замечание 2. Так как величина 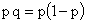 достигает максимума 0,25 при
достигает максимума 0,25 при 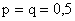 , то
, то
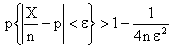 .
.
Центральная предельная теорема в грубой формулировке выглядит так: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.
Сформулируем более точно.
Теорема. Пусть 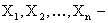 . независимые случайные величины с математическими ожиданиями
. независимые случайные величины с математическими ожиданиями 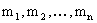 и дисперсиями
и дисперсиями 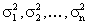 , причем
, причем
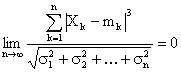 ,
,
то при 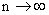 закон распределения случайной величины
закон распределения случайной величины 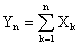 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.59. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время T равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время T окажется: а) меньшее двух; б) не меньше двух.
Решение. а) Пусть X — дискретная случайная величина, характеризующая число отказавших элементов за время T. Тогда
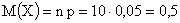 ;
; 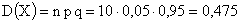 .
.
Воспользуемся неравенством Чебышева
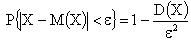 ;
; 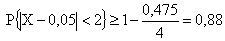 .
.
б) События 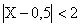 и
и 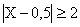 противоположны, поэтому
противоположны, поэтому 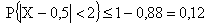 .
.
ПРИМЕР 13.2.60. Гнутая монета подбрасывается 100 раз. Герб выпал 70 раз. Оценим вероятность выпадения герба для этой монеты.
Решение. Возьмем 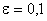 . Тогда получим
. Тогда получим
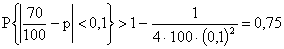 , то есть с вероятностью 0,75 оцениваемое значение
, то есть с вероятностью 0,75 оцениваемое значение 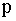 принадлежит интервалу
принадлежит интервалу 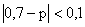 ;
;
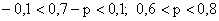 .
.
Для 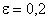 получим
получим 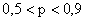 с вероятностью не менее 0,9375.
с вероятностью не менее 0,9375.
В качестве оценки p берем относительную частоту 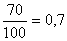 .
.
При увеличении числа испытаний n мы будем получать с вероятностью, близкой к единице, все более маленькие интервалы для оценки теоретической вероятности .
ПРИМЕР 13.2.61. На полосу укреплений противника сбрасывается 100 серий бомб. При сбрасывании одной такой серии математическое ожидание числа попаданий равно 2, а среднее квадратическое отклонение числа попаданий равно 1,5.
Найти приближенно вероятность того, что при сбрасывании 100 серий в полосу попадает от 180 до 220 бомб.
Решение. Представим общее число попаданий как сумму чисел попаданий бомб в отдельных сериях:
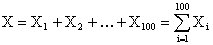 , где
, где 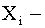 число попаданий i-ой серии.
число попаданий i-ой серии.
Будем считать число 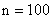 достаточным для того, чтобы можно было применить предельную теорему. Имеем:
достаточным для того, чтобы можно было применить предельную теорему. Имеем: 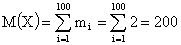 ;
;
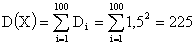 . СВ X подчинена нормальному закону распределения.
. СВ X подчинена нормальному закону распределения.
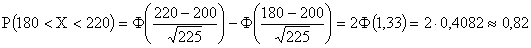 .
.
ПРИМЕР 13.2.62. Последовательность независимых случайных величин 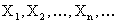 задана законом распределения
задана законом распределения
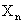 |
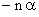 |
0 | 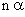 |
| P | 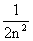 |
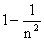 |
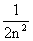 |
Применима ли к заданной последовательности теорема Чебышева?
Решение. Проверим конечность математических ожиданий и равномерную ограниченность дисперсий.
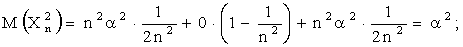 .
.
Таким образом, каждая из случайных величин 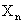 имеет конечное математическое ожидание.
имеет конечное математическое ожидание.
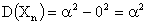 .
.
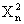 |
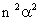 |
0 | 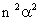 |
| P | 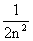 |
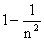 |
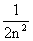 |
Так как все дисперсии равны, то они равномерно ограничены числом 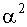 . Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.
. Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.
ПРИМЕР 13.2.63. В кассе учреждения имеется сумма 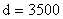 (руб.). В очереди стоит
(руб.). В очереди стоит 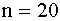 лиц. Сумма X, которую надо выплатить отдельному лицу – случайная величина с математическим ожиданием
лиц. Сумма X, которую надо выплатить отдельному лицу – случайная величина с математическим ожиданием 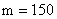 (руб.) и средним квадратическим отклонением
(руб.) и средним квадратическим отклонением 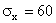 (руб.).
(руб.).
Найти вероятность того, что суммы d не хватит для выплаты денег всем людям, стоящим в очереди.
Решение. На основании центральной предельной теоремы для одинаково распределенных слагаемых при большом (n=20 практически можно считать «большим»), случайная величина 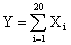 , где
, где 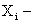 сумма, которую надо выплатить i-ому лицу, имеет приближенно нормальное распределение с параметрами
сумма, которую надо выплатить i-ому лицу, имеет приближенно нормальное распределение с параметрами
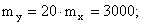 ;
; 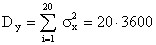 .
.
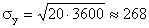 .
.
Суммы Y не хватит, следовательно, 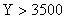 .
.
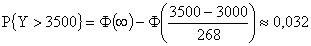 .
.
Итак, с вероятностью около 3% имеющейся в кассе суммы не хватит для выплаты всем, стоящим в очереди.
Примеры и задачи для самостоятельного решения
Решить задачи на предельные теоремы теории вероятностей
3.2.14.1. Пользуясь неравенством Чебышева, оценить вероятность того, что любая случайная величина отклонится от своего математического ожидания: а) менее чем на три среднеквадратических отклонения; б) не менее, чем на 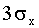 , в) не менее, чем на
, в) не менее, чем на 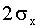 .
.
Отв.: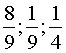
3.2.14.2. Дискретная случайная величина X задана законом распределения
| X | 0,1 | 0,4 | 0,6 |
| P | 0,2 | 0,3 | 0,5 |
Используя неравенство Чебышева, оценить вероятность того, что 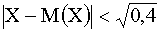 .
.
Отв.: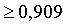
3.2.14.3. Вероятность появления события в каждом испытании равна 1/4. Используя неравенство Чебышева, оценить вероятность того, что число X появлений события заключено в пределах от 150 до 250, если будет произведено 800 испытаний. Сравнить с результатом вычисления по интегральной теореме Лапласа.
Отв.: 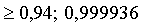
3.2.14.4. Дано 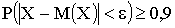 и
и 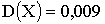 . Используя неравенство Чебышева, найти
. Используя неравенство Чебышева, найти 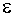 .
.
Отв.: 0,3
3.2.14.5. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время T лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время T окажется: а)меньше трех; б)не меньше трех.
Отв.: 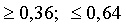
3.2.14.6. Сколько раз необходимо подбросить монету, чтобы вероятность отклонения относительной частоты выпадения «герба» от 1/2 на величину, не превосходящую 0.1, была бы не менее 0.9?
Отв.: 250 и более раз
3.2.14.7. Последовательность независимых случайных величин 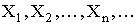 задана законом распределения
задана законом распределения
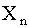 |
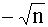 |
0 | 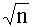 |
| P | 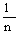 |
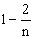 |
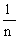 |
Применимо ли к заданной последовательности теоремы Чебышева?
Отв.: Применима
3.2.14.8. Ответить на вопрос задачи 3.2.14.7 для последовательности случайных величин
| X | -a | a |
| P | 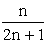 |
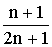 |
3.2.14.9. В условиях примера 2.14.5 определить: какую сумму a нужно иметь в кассе для того, чтобы вероятность того, что ее не хватит для выплаты всем стоящим, стала равна 0,005?
Отв.: 3691
3.2.14.10. Железнодорожный состав состоит из вагонов; вес каждого вагона в тоннах – случайная величина с математическим ожиданием 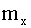 и средним квадратическим отклонением
и средним квадратическим отклонением 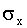 . Число вагонов n — большое (несколько десятков). Локомотив может везти вес не больше q (тонн); если вес состава больше q (тонн), приходится прицеплять второй локомотив. Найти вероятность того, что одного локомотива не хватит для перевозки состава.
. Число вагонов n — большое (несколько десятков). Локомотив может везти вес не больше q (тонн); если вес состава больше q (тонн), приходится прицеплять второй локомотив. Найти вероятность того, что одного локомотива не хватит для перевозки состава.
Отв.: 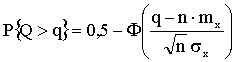
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >