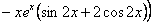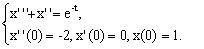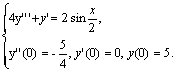Частное решение уравнения n-го порядка

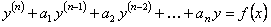,  (11.2.20)

где 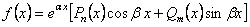, (11.2.21)

а a₁a₂,…,a_n 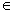R следует искать в виде

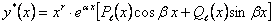.  (11.2.22)

Здесь r — кратность корня 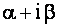в характеристическом уравнении

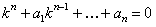.  (11.2.23)

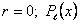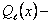Если (11.2.23) такого корня не имеет, то и полные многочлены от x степени 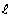, с неопределенными коэффициентами, причем 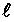равно наибольшему из чисел n и m .

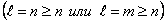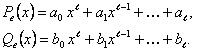  (11.2.24)

Неизвестные коэффициенты равенства (11.2.24) находятся из системы линейных алгебраических уравнений, получаемых отождествлением коэффициентов подобных членов в правой и левой частях исходного уравнения после подстановки в него y* вместо y.

Если правая часть уравнения (11.2.20) есть сумма конечного число функций вида (11.2.21), то частное решение есть сумма частных решений, соответствующих правых частей, т.е. если

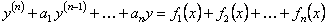,  (11.2.25)

то 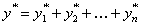, где y*₁ частное решение уравнения 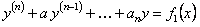и так далее.

ПРИМЕР 11.2.118 Найти общее решение уравнения .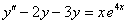

Решение.

По теореме о структуре общего решения неоднородного уравнения 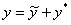. Найти 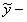общее решение соответствующего однородного уравнения 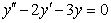. Его характеристическое уравнение имеет вид 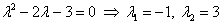, тогда .

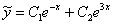Найдем частное решение по виду правой части 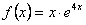. В данном случае .

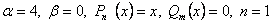Число 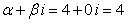корнем характеристического уравнения не является, значит 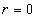. Согласно (11.2.22) частное решение будет иметь вид

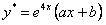. Для подстановки в данное уравнение найдем 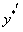и .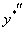

.

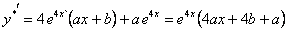
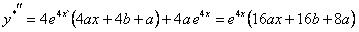
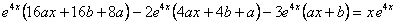Сокращая на e^4x и приравнивая коэффициенты при одинаковых степенях

x, получим .

Окончательно имеем .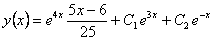

ПРИМЕР 11.2.119 Найти общее решение уравнения линейного осциллятора без трения с периодической внешней силой sin(ωt)

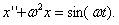
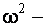частота собственных колебаний,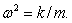

Решение.

Общее решение однородного уравнения 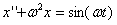выписывается с учетом корней характеристического уравнения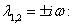

.

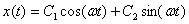Число 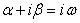, соответствующее правой части уравнения, является корнем характеристического уравнения, поэтому частное решение ищем в виде

.

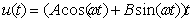
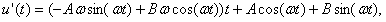
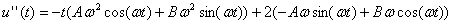После подстановки в уравнение получаем

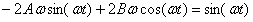
Отсюда 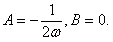Окончательно, общее решение неоднородного уравнения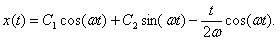

Наличие в общем решении членов пропорциональных t свидетельствует о росте со временем амплитуды колебаний. Этот эффект называется резонансом. Это происходит при совпадении частоты внешнего воздействия с собственной частотой.

Если правая часть уравнения представляет собой сумму различных функций вида (функций с разными α и β), то решение выписывается с использованием теоремы о суперпозиции решений: надо найти частные решения, соответствующие различным частям и затем взять их сумму, которая и является решением исходного уравнения.

ПРИМЕР 11.2.120 Найти общее решение уравнения 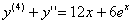с начальными данными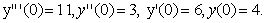

Решение.

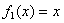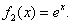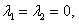
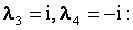
Сначала находится общее решение, затем определяются содержащиеся в нем произвольные константы. Правая часть представляет собой сумму двух функций и Для каждой из функций найдем  соответствующее частное решение. Общее решение y₀₀(x) однородного уравнения найдем согласно корням характеристического уравнения: 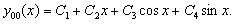Частное решение неоднородного уравнения будем искать в виде суммы двух функций 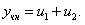Правой части f₁(x) соответствует 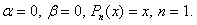Так как 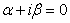— корень характеристического уравнения кратности 2, то решение ищем в виде многочлена первой степени 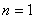с произвольными коэффициентами, умноженного на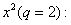

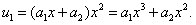
Правой части 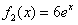соответствует 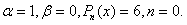Число 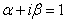корнем характеристического уравнения не является, следовательно, решение ищем в виде 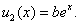Таким образом,

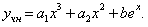
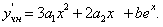
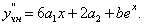
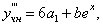
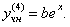
Подставляем в исходное неоднородное уравнение, получаем

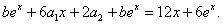
Отсюда 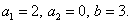Общее решение неоднородного уравнения

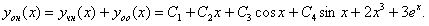
Найдем частное решение, соответствующее начальным данным. Для этого находим значение функции y(x) и ее производных при x=0 и приравниваем их к соответствующим начальным данным

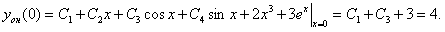
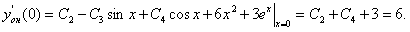
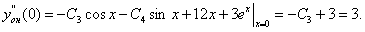
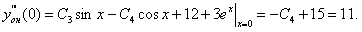
Отсюда немедленно следует 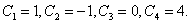Окончательно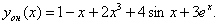

Примеры и задачи для самостоятельного решения

11.2.121	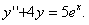Отв.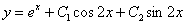
11.2.122	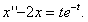Отв.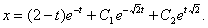
11.2.123	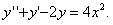Отв.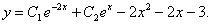
11.2.124	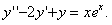Отв.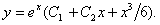
11.2.125	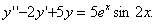Отв.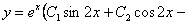
Решить задачу Коши:
11.2.126	Отв.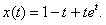
11.2.127	Отв.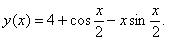
11.2.128	Отв.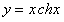

11.2.129 Определить закон движения материальной точки массы m, перемещающейся по прямой под влиянием восстанавливающей силы, направленной к началу отсчета перемещений и прямо пропорциональной расстоянию точки от начала отсчета, если сопротивление среды отсутствует, а на точку действует внешняя сила .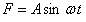

Отв. 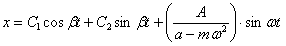, если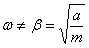

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >