Пусть дана функция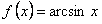 
. Требуется разложить ее в ряд Маклорена. Для решения поставленной задачи воспользуемся разложением (12.1.68) из 12.1.24, заменив в нем x на 
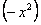, получим
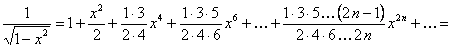
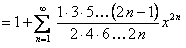. (12.1.69)
Ряд (12.1.69) можно почленно интегрировать при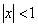 
на основании теоремы о почленном интегрировании степенного ряда, тогда
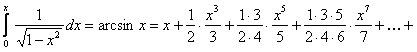
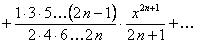(12.1.70)
Ряд (12.1.70) сходится в интервале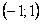 
. отметим без доказательства, что данный ряд сходится и при 
.
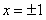Пусть дана функция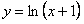 
. Требуется разложить ее в ряд Маклорена. Для решения поставленной задачи проинтегрируем ряд (12.1.61) от 
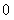до 
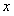, где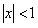 
. На основании теоремы о почленном интегрировании, получим
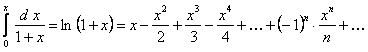(12.1.71)
Ряд (12.1.71) сходится в интервале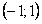 
, причем он сходится и при 
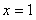(без доказательства).
Если в (12.1.71) заменить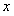 
на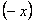 
, то получим разложение функции 
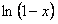в степенной ряд, то есть
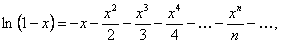(12.1.72)
где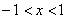 
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
