Рассмотрим линейное дифференциальное уравнение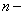 
го порядка вида
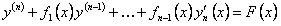. (12.1.78)
ТЕОРЕМА 12.1.18 Если коэффициенты и правая часть дифференциального уравнения (12.1.78) разлагается в степенные ряды по степеням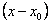 
, сходящиеся в некоторой окрестности 
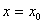, то решение этого уравнения, удовлетворяющее начальным условиям
(
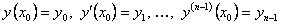
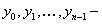произвольно заданные числа), разлагается в степенной ряд по степеням 
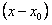, сходящийся, по крайней мере, в меньшем из интервалов сходимости рядов для коэффициентов и правой части дифференциального уравнения.
Практически решение дифференциального уравнения в виде степенного ряда можно получить двумя способами: сравнением коэффициентов и последовательным дифференцированием.
Способ сравнения коэффициентов заключается в следующем:
а) записываем решение в виде степенного ряда с неопределенными коэффициентами
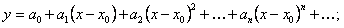(12.1.79)
б) из начальных условий определяем значения коэффициентов
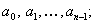
в) подставляем в дифференциальное уравнение вместо y и производных соответствующие степенные ряды, а также вместо коэффициентов и правой части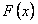 
записываем их разложения в степенные ряды по степеням 
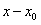и производим действия над рядами;
г) приравниваем коэффициенты при одинаковых степенях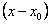 
, откуда находим неизвестные коэффициенты искомого ряда.
ПРИМЕР 12.1.24 Найти решение дифференциального уравнения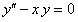 
, удовлетворяющее начальным условиям 
.
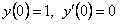Решение. Записываем решение в виде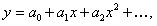 
так как 
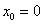. Из начальных условий определяем 
:
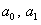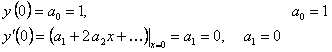
От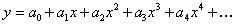 
(12.1.80)
находим y’ и y» и подставляем в данное уравнение:
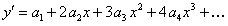
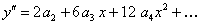
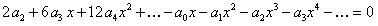
или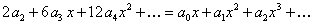 
.
Сравним коэффициенты при одинаковых степенях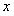 
; получим
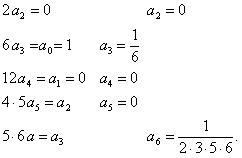
Найденные коэффициенты подставим в (12.1.80); получим ряд
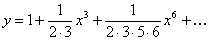
Полученный ряд, как это следует из теоремы (12.1.78), сходится при всех значениях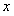 
.
Способ последовательного дифференцирования заключается в следующем:
а) искомое решение разлагают в ряд Тейлора по степеням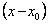 
:
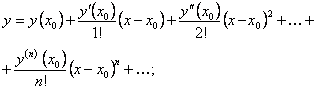
б) первые n коэффициентов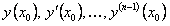 
заданы начальными условиями. Подставляя в уравнение 
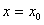, определяем 
;
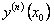в) последовательно дифференцируя уравнение и подставляя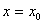 
, определяем коэффициенты ряда искомого решения.
ПРИМЕР 12.1.25 Найти решение дифференциального уравнения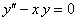 
при начальных условиях 
.
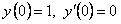Решение. Запишем решение уравнения в виде
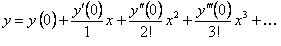
По условию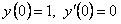 
. Подставим в дифференциальное уравнение 
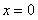, получим 
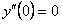. Будем последовательно дифференцировать уравнение 
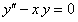и подставлять значение 
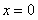, тогда
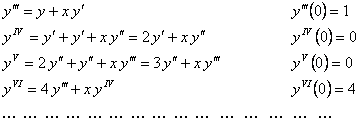
Полученные значения производных подставим в выражение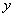 
.
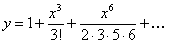
Таким образом, если дифференциальное уравнение не сводится к квадратурам, то прибегают к приближенным методам интегрирования. Одним из таких методов является представление решения уравнения в виде ряда Тейлора.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >