ТЕОРЕМА 12.1.10 Почленное интегрирование функциональных рядов.
Если функции 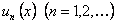 непрерывны на отрезке
непрерывны на отрезке 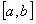 и составленный из них ряд
и составленный из них ряд 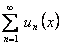 сходится равномерно на этом отрезке, и имеет суммой функцию
сходится равномерно на этом отрезке, и имеет суммой функцию 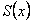 , то ряд составленный из интегралов от его членов на отрезке
, то ряд составленный из интегралов от его членов на отрезке 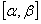 , также сходится и имеет суммой функцию
, также сходится и имеет суммой функцию 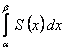 , где
, где 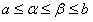 .
.
Доказательство. В силу равномерной сходимости функционального ряда 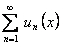 функция
функция 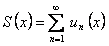 непрерывна на отрезке
непрерывна на отрезке 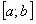 и поэтому интегрируема на любом отрезке с концами в точках
и поэтому интегрируема на любом отрезке с концами в точках  и
и 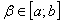 . Функцию S(x) можно представить в виде
. Функцию S(x) можно представить в виде 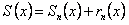 , где
, где 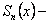 частичная сумма,
частичная сумма, 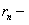 остаток ряда, или
остаток ряда, или
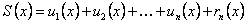 .
.
Тогда
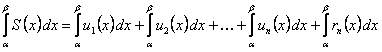 (12.1.33) (интеграл от суммы конечного числа слагаемых равен сумме интегралов от этих слагаемых). Таким образом, сумма
(12.1.33) (интеграл от суммы конечного числа слагаемых равен сумме интегралов от этих слагаемых). Таким образом, сумма 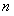 членов ряда
членов ряда 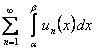 отличается от интеграла
отличается от интеграла 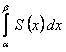 дополнительным членом
дополнительным членом 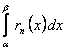 . Для доказательства теоремы нужно лишь установить, что
. Для доказательства теоремы нужно лишь установить, что 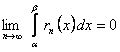 . В силу равномерной сходимости ряда
. В силу равномерной сходимости ряда 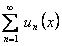 для
для 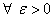 найдется номер
найдется номер 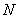 такой, что при
такой, что при 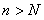
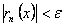 сразу для всех
сразу для всех 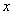 в рассматриваемом промежутке. Поэтому
в рассматриваемом промежутке. Поэтому
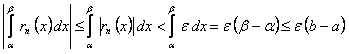 .
.
Так как при 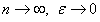 , то
, то 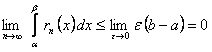 и из (12.1.33) получим
и из (12.1.33) получим
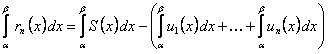 . (12.1.34)
. (12.1.34)
В (12.1.34) перейдем к пределу при 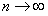 , получим
, получим
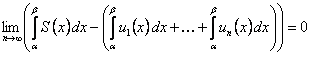 (12.1.35)
(12.1.35)
в силу (12.1.33) имеем
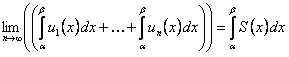 . (12.1.36)
. (12.1.36)
Сумма, стоящая слева в равенстве (12.1.36), есть частичная сумма ряда 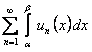 , она имеет конечный предел. Следовательно, ряд сходится и его сумма равна
, она имеет конечный предел. Следовательно, ряд сходится и его сумма равна 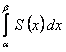 .
.
Тем самым доказаны сходимость ряда 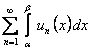 и равенство его суммы интегралу
и равенство его суммы интегралу 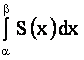 .
.
ПРИМЕР 12.1.13 Функциональный ряд 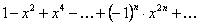 сходится равномерно при
сходится равномерно при 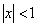 , так как при
, так как при 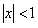 ряд является геометрической прогрессией со знаменателем меньше
ряд является геометрической прогрессией со знаменателем меньше 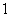 , сумма его равна
, сумма его равна 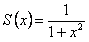 .
.
Проинтегрируем данный ряд от  до
до 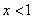 , в результате чего получим ряд
, в результате чего получим ряд
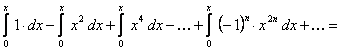
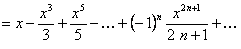 .
.
Полученный ряд сходится равномерно при 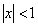 , согласно признаку Вейерштрасса. Тогда сумма полученного ряда
, согласно признаку Вейерштрасса. Тогда сумма полученного ряда 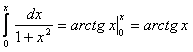 .
.
ТЕОРЕМА 12.1.11 Почленное дифференцирование функциональных рядов Пусть ряд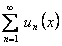 сходится на отрезке
сходится на отрезке 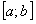 и имеет сумму
и имеет сумму 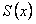 , а его члены имеют на этом отрезке непрерывные производные, причем ряд, составленный из этих производных
, а его члены имеют на этом отрезке непрерывные производные, причем ряд, составленный из этих производных 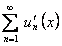 , сходится равномерно на
, сходится равномерно на 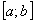 и имеет сумму
и имеет сумму 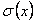 . Тогда функциональный ряд
. Тогда функциональный ряд 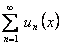 сходится на отрезке
сходится на отрезке 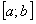 равномерно и производная его суммы равна сумме ряда
равномерно и производная его суммы равна сумме ряда 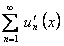 , то есть
, то есть 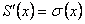 .
.
Доказательство. Так как ряд 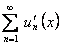 сходится равномерно на отрезке
сходится равномерно на отрезке 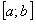 , то на основании теоремы (1) его можно почленно интегрировать от
, то на основании теоремы (1) его можно почленно интегрировать от 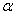 до x, где
до x, где 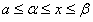 .
.
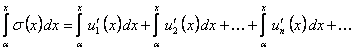
или 
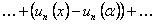 . По условию теоремы ряд
. По условию теоремы ряд 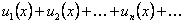 сходится и его сумма равна
сходится и его сумма равна 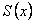 ; сходится по условию и ряд
; сходится по условию и ряд 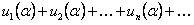 , его сумма равна
, его сумма равна 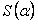 , тогда сходится и ряд
, тогда сходится и ряд 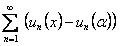 . Поэтому
. Поэтому
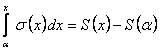 . Дифференцируя по
. Дифференцируя по 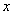 обе части равенства, получим
обе части равенства, получим
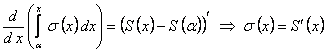 .
.
Остается доказать, что ряд 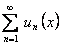 при выполнении условий теоремы равномерно сходится на отрезке
при выполнении условий теоремы равномерно сходится на отрезке 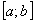 . Из равенства
. Из равенства
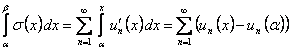 в силу доказанной сходимости рядов
в силу доказанной сходимости рядов 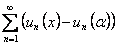 и
и 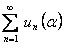 следует, что
следует, что
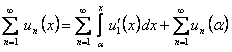 , но ряд
, но ряд 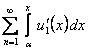 равномерно сходится на отрезке
равномерно сходится на отрезке 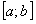 на основании теоремы 9, а
на основании теоремы 9, а 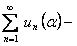 сходящийся числовой ряд, то есть ряд
сходящийся числовой ряд, то есть ряд 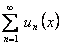 , равномерно сходится на отрезке
, равномерно сходится на отрезке 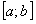 . Таким образом, при выполнении условий ряд
. Таким образом, при выполнении условий ряд 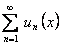 равномерно сходится на отрезке
равномерно сходится на отрезке 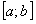 и производная от суммы ряда равна сумме производных от членов ряда.
и производная от суммы ряда равна сумме производных от членов ряда.
ПРИМЕР 12.1.14 Дан сходящийся на всей числовой оси функциональный ряд 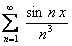 , сумма которого
, сумма которого 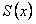 . Ряд, составленный из производных, то есть полученный из данного дифференцированием его членов
. Ряд, составленный из производных, то есть полученный из данного дифференцированием его членов 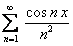 , равномерно сходится на всей числовой оси, согласно признаку Вейерштрасса.
, равномерно сходится на всей числовой оси, согласно признаку Вейерштрасса.
Показать, что 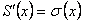 , где
, где 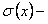 сумма ряда
сумма ряда 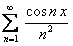 . Данный
. Данный
ряд 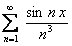 и ряд
и ряд 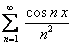 удовлетворяют условиям теоремы 12.1.10
удовлетворяют условиям теоремы 12.1.10
Следовательно, по доказанной теореме 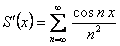 , то есть
, то есть 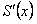 равна
равна 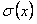 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >