Для определения коэффициентов ряда укажем прием, который во второй половине XVIII века был применен Эйлером и независимо от него в начале XIX века – Фурье.
Предположим, что функция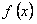 
абсолютно интегрируема на отрезке 
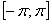, то есть 
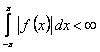имеет место разложение
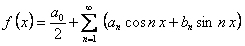(12.1.87)
и числовой ряд вида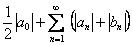 
сходится.
Тогда ряд (12.1.87) равномерно сходится и, следовательно, его можно интегрировать почленно в промежутке от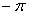 
до 
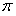. Используем это для вычисления коэффициента 
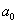. Проинтегрируем обе части равенства в пределах от 
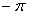до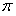 
:
.
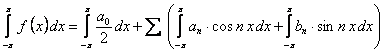Вычислим каждый интеграл отдельно
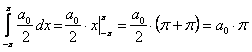. (12.1.88)
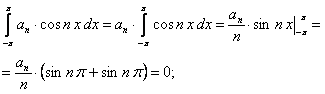(12.1.89)
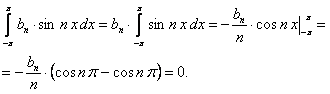(12.1.90)
Таким образом, с учетом (12.1.87), (12.1.88), (12.1.89) равенство (12.1.90) примет вид
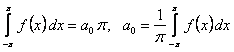. (12.1.91)
Для определения коэффициентов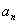 
и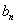 
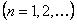нам понадобятся определенные интегралы
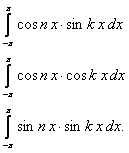(12.1.92)
Рассмотрим следующие случаи:
1) пусть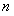 
и 
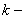целые числа и 
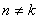, тогда
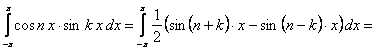
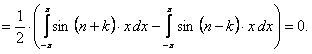(12.1.93)
(в силу нечетности функци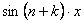и 
и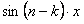 
)
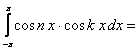
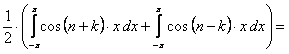
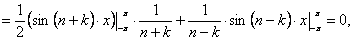
так как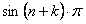 
и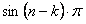 
равны нулю. (12.1.94)
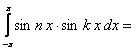
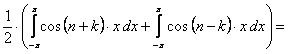
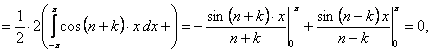(12.1.94)
так как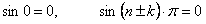 
;
2) пусть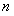 
и 
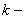целые числа и 
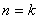, тогда
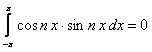(12.1.95)
в силу нечетности подынтегральной функции.
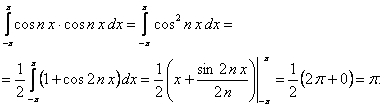(12.1.96)
(12.1.97)
Теперь мы можем вычислить коэффициенты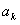 
и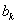 
.
Для отыскания коэффициента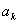 
при каком-либо определенном значении 
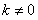умножим обе части равенства (12.1.87) на 
:
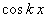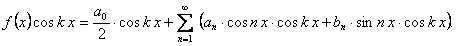(12.1.98)
В силу равномерной сходимости (12.1.98) его можно почленно проинтегрировать в пределах от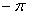 
до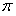 
.
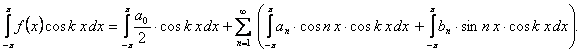(12.1.99)
Принимая во внимание (12.1.89), (12.1.93), (12.1.94), (12.1.95), (12.1.96), нетрудно заметить, что все интегралы в правой части (12.1.99) равна нулю, кроме интеграла с коэффициентом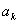 
. Следовательно,
,
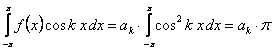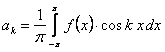.(12.1.100)
Аналогично умножая обе части (1) на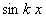 
и почленно интегрируя от 
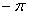до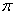 
, получим
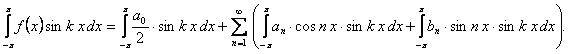(12.1.101)
В силу (12.1.90), (12.1.92), (12.1.94), (12.1.95), (12.1.97) все интегралы правой части (12.1.101) равны нулю, кроме интеграла с коэффициентом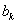 
.
Следовательно,
,
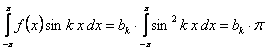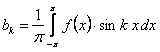.(12.1.102)
Коэффициенты, определенные по формулам
.
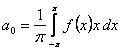
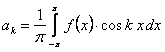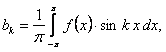
называется коэффициентами Фурье функции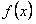 
, а тригонометрический ряд (12.1.87) с такими коэффициентами называется рядом Фурье функции 
.
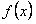Выясним, какими свойствами должна обладать функция, чтобы построенный для нее ряд Фурье сходился и, чтобы сумма построенного ряда Фурье равнялась значениям данной функции в соответствующих точках.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
