Признак Коши: Если для ряда с положительными членами
, 
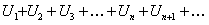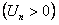величина 
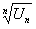имеет конечный предел 
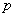при 
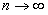, то есть
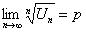, то
1) при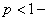 
ряд сходится;
2) при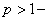 
ряд расходится;
3) при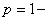 
этот признак не дает возможности определить сходимость или расходимость ряда.
Доказательство. 1. Пусть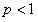 
. Рассмотрим число 
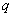, удовлетворяющее соотношению 
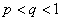. Начиная с некоторого номера 
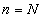, будет иметь место соотношение 
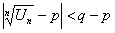, откуда следует, что 
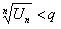или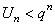 
для всех 
.
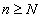Рассмотрим два ряда
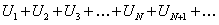(12.1.15)
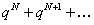(12.1.16)
Так как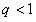 
, то ряд (12.1.16) сходится. Члены ряда (12.1.15) меньше соответствующих членов ряда (12.1.16), начиная с 
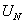. Следовательно, ряд (12.1.15) сходится на основании признака сравнения.
2. Пусть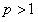 
. Тогда, начиная с некоторого 
, 
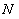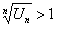или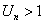 
, то есть не выполняется необходимое условие сходимости ряда, ряд сходится.
ПРИМЕР 12.1.5 Исследовать сходимость ряда
.
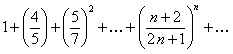Решение. Определим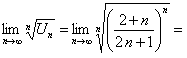 
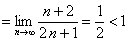, ряд сходится.
Замечание. Признаки Даламбера и Коши основаны на сравнении данного ряда с рядом геометрической прогрессии. Эти признаки не являются чувствительными к рядам, сходящимся медленнее, чем геометрическая прогрессия. Для таких рядов рассматривают более сильные признаки, в частности, интегральный признак Коши.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
