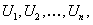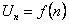Рассмотрим числовую последовательность где . Построим из этой последовательности выражение .

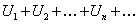ОПРЕДЕЛЕНИЕ 12.1.1 Выражени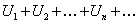е , где 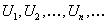— члены бесконечной числовой последовательности, называется числовым рядом.

Числа 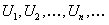называются членами ряда, а  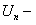 общим членом ряда. Для обозначения ряда применяют следующие записи:

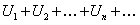 (12.1.1)

или

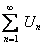.(12.1.2)

Зная общий член ряда, можно записать любой член ряда.

ПРИМЕР 12.1.1 Дан общий член ряда 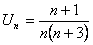. Написать первые три члена ряда и 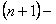й член.

Решение. Если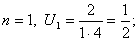

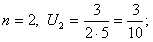
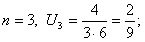
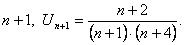
ОПРЕДЕЛЕНИЕ 12.1.2 Сумма 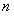первых членов ряда называется 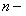й частичной суммой ряда.

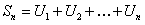.(12.1.3)

Очевидно, первая, вторая, третья и т.д. частичные суммы будут иметь вид

.

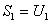
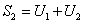
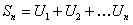ОПРЕДЕЛЕНИЕ 12.1.3 Ряд называется сходящимися, если существует конечный предел частичной суммы при 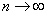, то есть

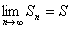.(12.1.4)

Число S называется суммой ряда.

ОПРЕДЕЛЕНИЕ 12.1.4 Ряд называется расходящимся, если предел частичной суммы не существует или равен бесконечности при .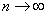

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >