Пусть производится n независимых испытаний, в каждом из которых событие А может появиться, либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность не появления q=1-p). Рассмотрим в качестве дискретной случайной величины Х число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения Х и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: .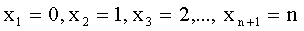

Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

,

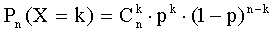где k=0, 1, 2, …, n.

Формула Бернулли и является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (1.26) можно рассматривать, как общий член разложения бинома Ньютона:.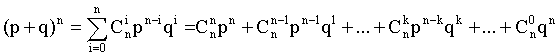

Таким образом, первый член разложения 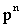определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй член 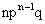определяет вероятность наступления события n-1 раз; последний член 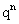определяет вероятность того, что событие не появится ни разу.

Напишем биномиальный закон в виде таблицы:

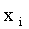	n	n-1	…	k	…	0
			…		…

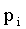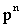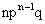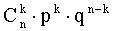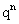Биномиальное распределение имеет, например, случайная величина X, выражающая число бракованных изделий в повторной выборке из n изделий или число очков, выбиваемых стрелком при стрельбе по мишени (см. пример 13.1.25) и т.д.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >