Используя функцию распределения системы случайных величин X и Y, легко найти вероятность того, что в результате испытания случайная точка попадет в полуполосу 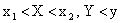
 .
.
или в полуполосу 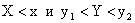
 .
.
.
Вычитая из вероятности попадания случайной точки в квадрант с вершиной 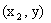 вероятность попадания точки в квадрант с вершиной
вероятность попадания точки в квадрант с вершиной 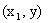 , получим
, получим
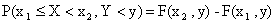 .
.
Аналогично имеем 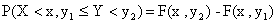 .
.
Таким образом, вероятность попадания случайной величины в полуполосу равна приращению функции распределения по одному из аргументов.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >