Рассмотрим дискретную случайную величину X с возможными значениями
.
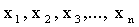В результате опыта величина X примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий
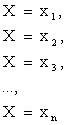
Обозначим вероятности этих событий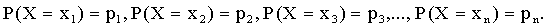 
Так как несовместные события образуют полную группу, то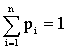 
, т.е. сумма вероятностей всех возможных значений равна единице. Эта суммарная вероятность каким-то образом распределена между отдельными значениями.
Случайная величина будет полностью описана с вероятностной точки зрения, если будет задано это распределение, т.е. в точности будет указано, какой вероятностью обладает каждое из событий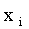 
. Этим устанавливается т.н. закон распределения случайной величины.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:
| X |  |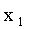
 |
… |  |
 |
 |
 |
… |  |
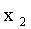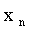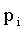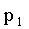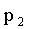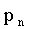Если множество возможных значений Х бесконечно (счетно), то ряд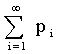 
сходится и его сумма равна единице.
ПРИМЕР 13.1.25 Стрелок производит три выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 5 очков. Найти закон распределения случайной величины Х — числа выбитых очков.
Решение. Напишем возможные значения X: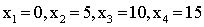 
.
Соответствующие вероятности этих возможных значений найдем по формуле Бернулли
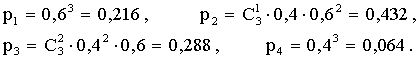
Напишем искомый закон распределения
| X | 0 | 5 | 10 | 15 |
 |
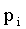0,216 | 0,432 | 0,288 | 0,064 |
Контроль: 0,216+0,432+0,288+0,064=1.
Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки
, а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения (рис. 13.1.2).
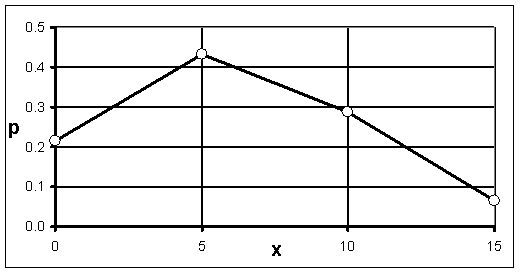
Среди законов распределения для дискретных случайных величин наиболее распространенными являются биномиальное распределение, распределение Пуассона, геометрическое распределение и некоторые другие.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
