На практике при решении задач приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы нормального, показательного и равномерного распределений.
Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при достаточно часто встречающихся типичных условиях.
Примерами случайных величин, имеющих нормальное распределение, могут служить: отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров, ошибки при измерении, отклонения при стрельбе и другие. Все эти примеры объединяет общая закономерность: случайная величина является результатом действия большого числа различных факторов, воздействие каждого из которых на данную величину незначительно и невозможно указать, какой именно влияет в большей степени, чем остальные.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
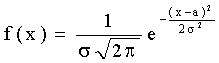 ,
,
Очевидно, что нормальное распределение определяется двумя параметрами: а и 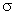 . Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание,
. Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, 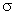 — среднее квадратическое отклонение нормального распределения.
— среднее квадратическое отклонение нормального распределения.
По определению математического ожидания непрерывной случайной величины
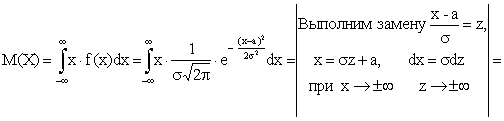 ,
,
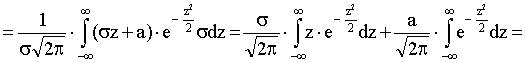 ,
,
 .
.
Итак, М (X) = а, т. е. математическое ожидание нормального распределения равно параметру а;
Далее, по определению дисперсии непрерывной случайной величины, учитывая, что М(Х)=а, имеем
 ,
,
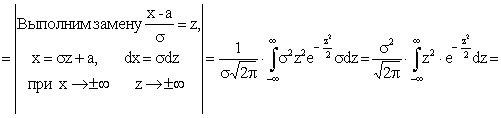 ,
,
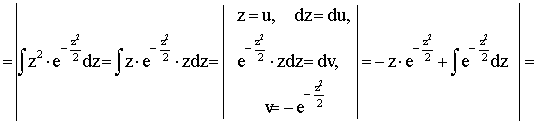 ,
,
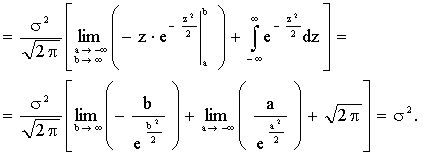 .
.
Итак,
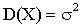
По определению математического ожидания непрерывной случайной величины
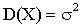 ,
,
Следовательно
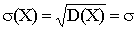
Таким образом, среднее квадратическое отклонение нормального распределения равно параметру 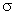
Замечание. Общим называют нормальное распределение с произвольными параметрами а и 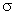 (
(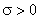 )
)
Нормированным называют нормальное распределение с параметрами а=0 и 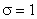 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >