Уже известно, что если случайная величина Х задана плотностью распределения
f(x), то вероятность того, что Х примет значение, принадлежащее интервалу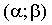 
, такова:
.
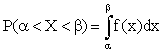Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу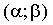 
, равна
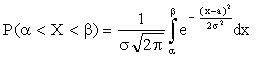
Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами.
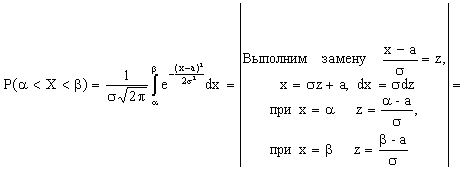
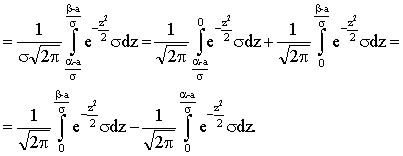
Пользуясь функцией Лапласа
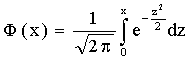
окончательно получим
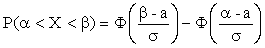
ПРИМЕР 13.1.46 Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10;50).
Решение. По условию,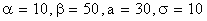 
, следовательно,
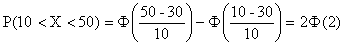
По таблице находим Ф(2)=0,4772. Отсюда искомая вероятность
.
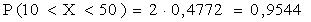Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
