При математической формализации модели испытания исходным является понятие пространства элементарных событий (обозначается 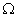), связанного с данным испытанием.

ПРИМЕР 13.1.10 Игральная кость бросается один раз. Обозначим 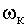событие, состоящее в выпадении к очков. Элементарными событиями в данном испытании являются события .

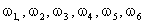Составные события, или просто события, могут быть описаны как подмножества множества элементарных событий: 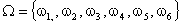. Например: событие А ={выпало четное число очков} через элементарные события выражается так: .

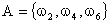ПРИМЕР 13.1.11 Испытание состоит в радиолокационном обнаружении цели. Событие – положение светящегося пятна (сигнала отраженного импульса от цели) на экране индикатора цели, имеющего форму круга радиуса 10 см, в декартовой системе координат с началом, совпадающим с центром экрана.

Пространство элементарных событий в этом испытании есть множество точек экрана: ,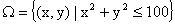
а элементарными событиями являются координаты случайной точки 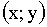на плоскости экрана.

Событие A={цель находится в первом квадранте} может быть записано в виде

.

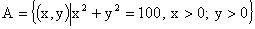Поле событий

В рассмотренных примерах элементарные события представляли собой все мыслимые взаимоисключающие исходы испытания. В общем случае пространством элементарных событий называется произвольное множество 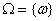, а элементы 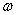этого множества называют элементарными событиями. Любое подмножество данного множества интерпретируется как событие (возможно, и не наблюдаемое). Совокупность всех наблюдаемых событий составляет поле событий для данного испытания.

Говорят, что событие А наступило, если результатом испытания оказалось событие 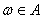. Событие, совпадающее с пустым множеством, называется невозможным событием, а событие, совпадающее со всем множеством , — достоверное событие.

Два события А и В совместны, если соответствующие множества А и В имеют общие элементы, и несовместны в противном случае.

Множество для данного испытания может быть дискретным (конечное или счетное множество) или непрерывным (множество типа континуума) (см. примеры 13.1.10, 13.1.11).

Алгебра событий

Так как событие отождествляется с элементом множества, то операции над событиями аналогичны операциям над множествами. В частности, определены следующие операции и отношения между событиями:

Отношение включения: (множество А является подмножеством множества В) – событие А влечет за собой событие В.

Отношение эквивалентности: А = В (эквивалентность множеств) – событие А тождественно событию В.

• 
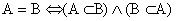
• А + В 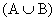(объединение множеств) — сумма событий.
• А В 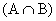(пересечение множеств) — произведение событий.
• А – В (А / В) (разность множеств) — разность событий.
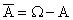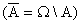• , (дополнение множества А до ) – противоположное событие. Событие 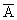означает, что событие А не произошло.

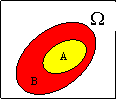
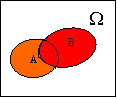
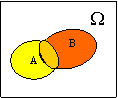
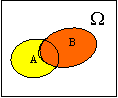
Условно изображая события в виде областей на плоскости, получим диаграммы Венна, которые иллюстрируют введенные определения. Наступление события А трактуется как попадание случайной точки в область, соответствующую этому событию.

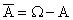Понятие произведения и суммы событий переносится на бесконечные последовательности событий:

.

.

.

.

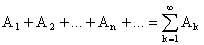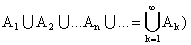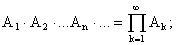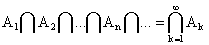Аксиоматическое определение вероятности

Приведем некоторые полезные тождества, которые вытекают из данных выше определений:

.

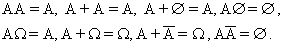Аксиомы теории вероятностей вводят таким образом, чтобы вероятность события А обладала всеми свойствами относительной частоты Р*(А). В этом случае теория вероятностей будет согласовываться с практикой.

Пусть F – поле событий для данного испытания. Вероятностью Р(А) называется числовая функция, определенная для всех 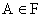и удовлетворяющая трем условиям (аксиомам) :

А1. Аксиома неотрицательности. Каждому событию 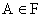сопоставлено неотрицательное число Р(А) : , .

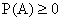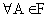А2. Аксиома нормированности. Вероятность достоверного события равна единице :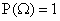

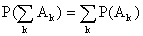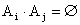А3. Аксиома аддитивности. Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий. , где , при .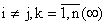

Опираясь на эти аксиомы, доказывают основные теоремы и формулы теории вероятностей. Математическая формализация модели испытания включает в себя:

1. построение пространства элементарных событий ,
2. описание поля событий F для данного испытания,
3. задание вероятностного распределения на поле событий.

Последний этап наиболее труден. Аксиомы теории вероятностей не содержат указаний о численных значениях вероятностей интересующих нас событий, а определяют лишь общие свойства, которыми должна обладать вероятность как числовая функция. Вопрос о том, какое значение вероятности следует приписать тем или иным событиям в реальных испытаниях, решается методами математической статистики.

В случае, когда пространство элементарных событий представляет собой конечное множество равновероятных исходов (схема урн) (т.е. 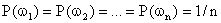), то испытание сводится к классической схеме или схеме урн. Поэтому вероятность события 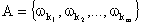определяется по формуле классической вероятности:
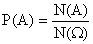, где N(A) – число случаев, благоприятных событию А, 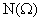— общее число случаев.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >