Свойство 1. Дисперсия постоянной величины С равна нулю:.
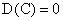 .
.
Данное свойство очевидно, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:.
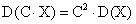 .
.
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:.
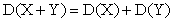 .
.
Данное свойство очевидно, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин..
Например, для трех слагаемых имеем:
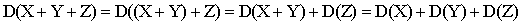 .
.
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:.
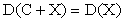 .
.
Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:.
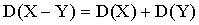 .
.
Рассмотрим следующую задачу. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна. Чему равна дисперсия числа появлений события в этих испытаниях? Ответ на этот вопрос дает следующая теорема.
ТЕОРЕМА 13.1.13. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
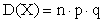 .
.
ПРИМЕР 13.1.38 Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X — числа появлений события в этих испытаниях.
Решение
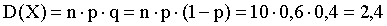 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >