Свойство 1. Значения функции распределения удовлетворяют двойному неравенству 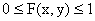 .
.
Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность – всегда неотрицательное число, не превышающее единицу.
Свойство 2. F(x,y) есть неубывающая функция по каждому аргументу, т.е.
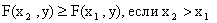 ;
;
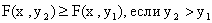 .
.
Доказательство. Докажем, что F(x,y) – неубывающая функция по аргументу x. Событие, состоящее в том, что составляющая X примет значение, меньшее 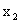 , и при этом составляющая Y < y, можно подразделить на следующие два несовместных события:
, и при этом составляющая Y < y, можно подразделить на следующие два несовместных события:
- X примет значение, меньшее
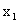 , и при этом Y < y с вероятностью
, и при этом Y < y с вероятностью
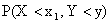 ;
; - X примет значение, удовлетворяющее неравенству
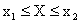 , и при этом Y < y с вероятностью
, и при этом Y < y с вероятностью 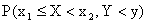 .
.
По теореме сложения,
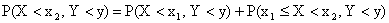 .
.
Отсюда
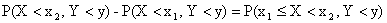 ,
,
или
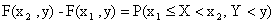 .
.
Любая вероятность есть число неотрицательное, поэтому 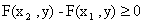 , или
, или 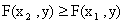 , что и требовалось доказать.
, что и требовалось доказать.
Свойство становится наглядно ясным, если воспользоваться геометрическим истолкованием функции распределения как вероятности попадания случайной точки в бесконечный квадрант с вершиной (x;y). При возрастании x правая граница этого квадранта сдвигается вправо; при этом вероятность попадания случайной точки в новый квадрант, очевидно, не может уменьшиться.

Аналогично доказывается, что F(x,y) есть неубывающая функция по аргументу y.
Свойство 3. Имеют место предельные соотношения:
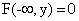 ,
,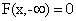 ,
,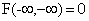 ,
,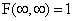 .
.
Доказательство
1) 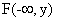 есть вероятность события
есть вероятность события 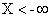 и Y < y; но такое событие невозможно (поскольку невозможно событие
и Y < y; но такое событие невозможно (поскольку невозможно событие 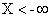 ), следовательно, вероятность этого события равна нулю.
), следовательно, вероятность этого события равна нулю.
Свойство становится наглядно ясным, если прибегнуть к геометрической интерпретации: при 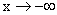 правая граница бесконечного квадранта неограниченно сдвигается влево и при этом вероятность попадания случайной точки в квадрант стремится к нулю.
правая граница бесконечного квадранта неограниченно сдвигается влево и при этом вероятность попадания случайной точки в квадрант стремится к нулю.
2) Событие 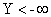 невозможно, поэтому
невозможно, поэтому 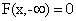 .
.
3) Событие 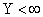 невозможно, поэтому
невозможно, поэтому 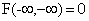 .
.
4) Событие 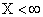 и
и 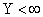 достоверно, следовательно, вероятность этого события
достоверно, следовательно, вероятность этого события 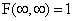 .
.
Свойство становится наглядно ясным, если принять во внимание, что при 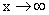 и
и 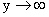 бесконечный квадрант превращается во всю плоскость xOy и, следовательно, попадание случайной точки (X;Y) в эту плоскость есть достоверное событие.
бесконечный квадрант превращается во всю плоскость xOy и, следовательно, попадание случайной точки (X;Y) в эту плоскость есть достоверное событие.
Свойство 4
а) При 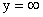 функция распределения системы становится функцией распределения составляющей X:
функция распределения системы становится функцией распределения составляющей X: 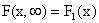
.
б) При 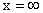 функция распределения системы становится функцией распределения составляющей Y:
функция распределения системы становится функцией распределения составляющей Y: 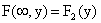 .
.
Доказательство.
а) Так как событие 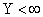 достоверно, то
достоверно, то 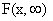 определяет вероятность события X
определяет вероятность события X
б) Доказывается аналогично.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >